意外とかんたん!?2進法

おはようございます、satoです。

今日は数学の話をしたいと思います。「2進法」という数字の表記法についてです。
以前書いたことがある「p進数」とは微妙に関係がある話です。
といっても、そこまで難しい話ではない…はずです。なんせ、コンピュータにも使われているなど、皆さんにとっても身近なものだから。

問題:私達の手でどれくらい数えられる？

私たちの手には10本の指がありますが、この指を使ってどれくらいの数字を数えられるでしょうか？
私達がいつもしているのは指を一つずつ折って1,2,3,4…と数えることですが、そうすると10までは数えられますよね？
しかし、実はもっと多く数えることができるのです！果たしてそれはどれくらいでしょうか？
答えはこの記事の最後に書きたいと思います。今日の記事を読んだら答えが理解できると思われます。

数字の表記法

さて、私達がいつも使っている数字は「0～9」の10種類があります。この10の数字を使って、もっと大きな数字を表記しています。具体的には1が十個集まると桁が一つ繰り上がるようにしています。これを「10」と表現しています。そして「10」が2つで「20」、3つで「30」、…10個集まると100と表現します。そして、10が2つと1が4つで「24」という感じで100までの数字を表現します。
以下、1000、10000…と続いていきます。この表記方法を「10進法」といいます。
みなさんが筆算をしている時にもこれを使っています。足し算をして10を超えたら1繰り上がり…というあれです。
ちなみに、10進法がよく使われているのは人の手が「10本の指」を持っているからだと思われます。

このように、「1がいくつか集まるごとに表記が変わる」ものがたくさんあります。
たとえば、時間は60秒で1分、60分で1時間というように60ごとに表記が変わります。これは「60進法」というわけです。
他にも12進法(1年は12ヶ月とか1ダースが12個とか)などが使われますね。

2進法とは

さて、私達が使っているいつも使っている数字は「0～9」の10個ですが、これを「0と1」だけにしてみましょう。そして「1が2個集まると桁が繰り上がる」ようにします。こうした表記法を2進法といいます。
コンピュータのビットは「電気が通ると1、通らないと0」というように動くので、まさに2進法が使われています。
ちなみに、MBがGBに上がる時に「1000」でなく「1024」なのは、上のビットの原理により「2の累乗」に合わせたほうがキレイだからです。実際です。

私達のいつも使っている10進法を2進法に置き換えると次のようになります。

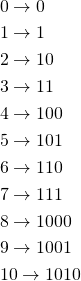
ただし、左がいつも使っている10進法、右が2進法による表記です。

2進法による数字が10進法ではどんな数なのかを考えるには次のように計算すればいいです。
10進法のときは

というように、一桁目の数字に、二桁目の数字に、三桁目の数字には…を掛けて足してあげています。これと同じように、2進法のときは

というように計算すればいいのです。

余談

ちなみに、2進法によって自然数はすべて表現できますが、もし「桁数が無限にあってもいい」としたらどうなるでしょうか？実数は「循環しない無限小数」ですが、それみたいに。
実はこれが「2進数」となります。正確には「2進整数」ですが。

問題の答え

さて、最初の問題「10本の指を使って最大いくつまで数えられるか？」の答えです。
私達の指は10本あって、いつもなら「0～9」を対応させて指を折ることで数えていました。
しかし、このようにすれば「0～1023」の1024個数えることができるのです。

まず、それぞれの指を折ったときを0、指を立てたときを1とします。
そして、左の指から2進法で一桁、二桁…とすると最大10桁の2進法数が出てきます。
つまり、指を折るのと立てるので、1024の数字を表現するのです。
たとえば、

このように親指を立てていたらですし、

この子みたいに、人差し指と中指を立てていたら、つまりピースをしていたらと表すことができます。
また

この男性のようにダブルピースをしているととなります。
こんなに数えられるなんて…人間ってすごいですね。

参考文献

小学生にn進法を分かりやすく説明しよう！-塾講師ステーション情報局（たぶん、こっちのほうが分かりやすいと思います）

この記事を書いたブロガー

sato

「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

最近の投稿

もっと見る

• 日常生活2024年4月19日韓国の「DUNKIN’ DOUNUTS」は美味しいのか？
• 私と発達障害2024年4月18日心が不調になった時の整え方
• 日々感じること2024年4月17日自分の理解の甘さを痛感した話
• 聖書＆御言葉2024年4月16日次元を上げたい、というところまで行かない私へ。