おはようございます、satoです。
以前「大学の個性」東工大編で「全てのことを厳密に考える」という話がありました。これは東工大が「世界最高の理工系総合大学の実現」を目指している工業系大学だから、なのかもしれません。工業には精密な視点と思考が必要ですからね。
前に記事を書いたときに東工大OGの方からツイッターでのイメージの大本は「2次試験の数学の配点が高い(なんと4割!!)」ことから来ているのではないか、という話を教えていただきました。なるほど確かに…4割は高いですね。これはどうしてか、というと…数学はとても厳密に考える学問だからです。
昨日たまたま見つけたツイッターのネタで、改めてそれがわかりました。
今日はそれをご紹介。
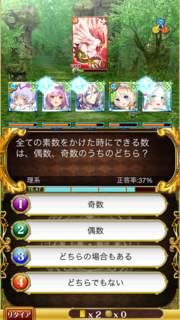
この答えはなんでしょう?
これはすざく(ペンギン)さんのツイートから取ってきたものです。このツイートを見る前に一度考えてみてください。
ところで、素数というのは「1とそれ以外の数以外に約数を持たない自然数」のことです。
小さいところから順に2,3,5,7,11,13…となります。
「素数の中に2が含まれるんだから、答えは偶数なんじゃないの?」
ゲームの答えでも偶数が答えでしたからね。
しかし。
そもそも「全ての素数の積」というものは数になるのでしょうか?
というのがこのツイートの面白い(あるいはややこしい)ところなのです。
順を追って説明します。
たとえば、2×3、2×3×5などのように「1からn番目の素数の積」はちゃんと答えがあって、それは6,30…と偶数になります。これは「有限個の積」だからです。ところが、「全ての素数の積」というように無限というものが絡むと、数学は一気に難しくなります。
数学では「無限個の素数の積」というものを「2×3、2×3×5,2×3×5×7,…」と掛ける個数を一つずつ増やしていって、近づく数があればそれを答えとして定義します。(すいません、数学的には厳密ではなく、そこまでわかりやすくもないという…)
で、素数の積というのは掛ける個数を増やしていくと…限りなく大きくなります。
こういう時、無限個の積は「無限大に発散する」と言います。
まとめると無限個の素数の積は一つの数にならないということなのです。
計算を間違えたら違った世界だ。
これは鄭明析先生の御言葉です。御言葉では「引くべきところを足したから答えが違ったのだ。」という話が出ていました。数学というのは計算を間違えると、全てが変わってしまう、それくらい厳密な学問なのです。
ちゃんとその計算が「適切」なのか考察しないと、今の問題のように答えを間違えてしまいます。これは人生でも同じ。
自分が今考えている、その考えは果たして「今の状況、この時」にふさわしいものなのか?
そこに気を付けながら、日々を送っていきたいですね。
ところで、この問題はそもそも問題として不適切、あるいは「どちらでもない」というのが答え…となりそうですが。
しかし、ツイッターの数学好き(数学徒と呼ばれています)はここで終わらなかった。彼らはこんなことを言い始めました。
それでは、この問題の「無限個の素数の積」というのはどういう意味なんだろう?
「無限個の素数の積」がちゃんと定義されるとしたら、それは偶数なのだろうか?
いや、さっき「無限個の素数の積は一つの数にならない」って言ったやん!
と突っ込みが入りそうですが。
…これ以上深く入ると、私も皆さんも頭が痛くなるので書きませんが。
無限個の積を色々解釈したり、収束するような数を定義することによって、この問題を考えることが出来るのです。数学って、とんでもなく複雑ですね。
…この話に興味を持った方は、「全ての素数の積が偶数なのが納得がいかない数学徒たち」を見てみてください。そこには数学の深淵さがありますから…。
(これは上記の記事を読めるくらい数学に精通している人向けです。)
「偶奇を判定する」ということは「余りを出す」必要があります。ということは、「全ての素数の積」が含まれている環には「余り付き割り算」が定義されている(つまり、ユークリッド環である)必要があるのでは?と安直なことを考えていました。
それ以外にも偶奇の判定法があるのかもしれませんが…そこは不勉強です(/_;)
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿

