おはようございます、satoです。
この記事はtsujimotterさん主催の日曜数学 Advent Calendar 2021 の9日目の記事になります。
前日の記事(離散編)に引き続き、統計に出てくる『確率分布』とは何かについて考察した記事になります。
目次 非表示
前回の復習
前回は以下のようなことをやりました。簡単におさらいしますと、
- 確率とは「ある物事の起こりやすさを数値化したもの」である。
- 確率を計算するときは「起こりうる結果全体に対する、その物事が起こる結果の割合」で計算する。割合というのがポイント。
- 確率分布とは「確率変数
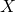 (起こりうる結果を数字にしたものを取る変数)に対して、『
(起こりうる結果を数字にしたものを取る変数)に対して、『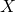 が起こる確率』を分布させたもの(関数)」である。
が起こる確率』を分布させたもの(関数)」である。
ということを書きました。この話に引き続き本日の記事を書いていきます。
(今回の内容も数学的事実に基づいて書いていますが、今回はより自分なりの解釈・考え方も多く入っています。そのあたりを理解の上読んでいただければと思います。
数学的なミスがありましたら、ぜひTwitter等でツッコんでいただけると幸いです)
離散から連続へ
さて、前回の話でもあったように、『コイントスを4回やって表が出る回数』は![]() のいずれかでした。特に分数や小数にはなりません(1/2回とか0.3回とかは考えられませんよね)。
のいずれかでした。特に分数や小数にはなりません(1/2回とか0.3回とかは考えられませんよね)。
この「回数」とか「個数」みたいに、値が自然数(0を含む)、または整数になるような量を「離散量」、それを扱う確率分布を「離散確率分布」といいます。
(余談ですが、前回の記事では当初「値が自然数となるものを離散」としました。
しかし、たとえばランダムウォーク(サイコロを振って奇数の目なら![]() 、偶数の目なら
、偶数の目なら![]() 進むとしたとき、これを
進むとしたとき、これを![]() 回繰り返すとどこに行くのか?という問題みたいなもの)は最終的な位置の座標を
回繰り返すとどこに行くのか?という問題みたいなもの)は最終的な位置の座標を![]() としたとき、
としたとき、![]() は整数の値になります。これも離散となるので、修正しました。)
は整数の値になります。これも離散となるので、修正しました。)
一方、値が自然数や整数で表し切れないものも多くあります。例として「インコの体重」を考えてみます。
インコの体重を測るときに、1g単位のキッチンスケールで測れば39gと出たとしましょう。
しかし、だからといってインコの実際の体重がきっちり39gというわけではありません。
0.1g単位で測れるキッチンスケールで測ると39.3gと出ることもあれば、39.0gと出るかもしれません。さらに0.01g単位で測れるものがあれば、より細かい数値が出てきます。
1羽のインコは必ず一定の体重を持つのですが、「キッチンスケールの単位が細かい(つまり、小数点以下を多く測れる)ほどインコの体重の真の値に近づく」ということが予想されます。
このように「単位を細かくするほど真の値に近づく」性質を持つものを「連続量」だと考えます。「連続」なものは実数で表します。
具体的には体重、身長、体積、速さ、時間…などですね。いくらでも細かくできるものが「連続」と考えていただけるとわかりやすいでしょうか。
いよいよ難関:連続確率分布
この連続なものを横軸として、先程のコイントスと同じような確率分布を考えたのが「連続確率分布」です。
※「連続確率分布」という単語は、本来は『累積分布関数が連続である』ような確率分布のことを表しております。今回考えるのは、正確には「確率変数が連続なときに考える確率分布」のことですが、「離散確率分布」との対比のためあえてこの単語を使います。
連続確率分布について勉強すると「インコの体重が39gである確率は0である」というような話が出てきます。
しかし、よくよく考えると「計測した体重が39gのインコ」は実際にいますよね。
実際にいるのに、どうして確率が0なのか?これについて、私なりに考えてみました。
連続な値における確率の考え方(の自分なりの捉え方)
インコの体重の例でも書いたように、連続量は「単位を細かくして計測するほど真の値に近づく」という性質があると話しました。そこで、連続量の確率分布を次のように考えます。
たとえば、インコの体重を1g単位で測るキッチンスケール(小数点以下切り捨て、と仮定します)で測ったところ39gだった、としましょう。すると、インコの真の体重は![]() の範囲に含まれます。
の範囲に含まれます。
そこで、「全体に対する ![]() の範囲の割合」を考えます。つまり「インコの体重の真の値になる確率」を考える代わりに「インコの体重を1g単位で計測したときに39gとなる確率」を考えるのです。
の範囲の割合」を考えます。つまり「インコの体重の真の値になる確率」を考える代わりに「インコの体重を1g単位で計測したときに39gとなる確率」を考えるのです。
もちろん、 インコの体重を0.1g単位で測るキッチンスケールで測るように、単位を細かくすると真の値が入る範囲も 狭まるので、それに応じて確率も変化します。
ここで「全体のうちある範囲がどれくらいの割合になるのか」を決める目安が必要になるのですが、それが「確率密度関数」となります。
確率密度関数
先程の「コイントス4回」の問題を振り返ると、![]() として横軸が
として横軸が![]() のところに「表が
のところに「表が![]() 回出る確率」を対応させたわけです。
回出る確率」を対応させたわけです。
この「表が![]() 回出る確率」というのは言い換えると「コイントスを4回したときに『表が
回出る確率」というのは言い換えると「コイントスを4回したときに『表が![]() 回出る』ということが全体のうちどれくらいの割合か」ということであり、「『表が
回出る』ということが全体のうちどれくらいの割合か」ということであり、「『表が![]() 回出る』のは全体の中でどれくらいの頻度か」ということを表している、とも言えます。
回出る』のは全体の中でどれくらいの頻度か」ということを表している、とも言えます。
これに対応するように、体重を![]() とおいたとき「体重が
とおいたとき「体重が![]() gであることが全体の中でどれくらいの頻度か」という値を対応させる関数を確率密度関数といいます。グラフで言うとこんな感じです。
gであることが全体の中でどれくらいの頻度か」という値を対応させる関数を確率密度関数といいます。グラフで言うとこんな感じです。
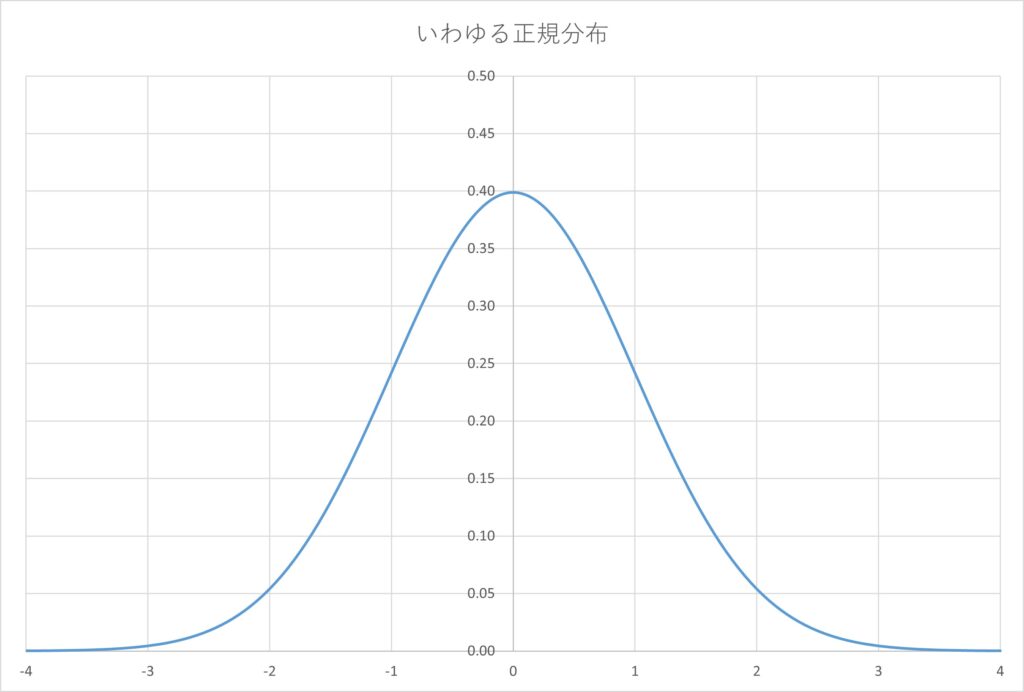
ここで注意なのは確率密度関数を![]() としたとき、たとえば、
としたとき、たとえば、![]() という数値は「39gはどれくらい起こりやすい」のかを表すもので、確率とは異なるということです。これは「コイントス4回」の問題のような離散な値の場合とは異なる部分です。
という数値は「39gはどれくらい起こりやすい」のかを表すもので、確率とは異なるということです。これは「コイントス4回」の問題のような離散な値の場合とは異なる部分です。
なので、![]() という値そのものにはあまり意味がありません。確率密度関数の値で大事なのは
という値そのものにはあまり意味がありません。確率密度関数の値で大事なのは
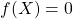 のとき、体重が
のとき、体重が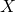 gになることは(ほぼ確実に)ない(たとえば、体重が負の値を取ることはないので
gになることは(ほぼ確実に)ない(たとえば、体重が負の値を取ることはないので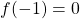 )
)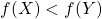 のとき、「体重が
のとき、「体重が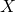 gになるより体重が
gになるより体重が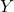 gになることの方が頻度が高い」
gになることの方が頻度が高い」- 頻度が負の値になることはないので、
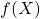 は
は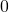 以上
以上 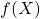 のグラフと横軸で囲まれた図形の面積が
のグラフと横軸で囲まれた図形の面積が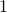 である(この理由は後述します)
である(この理由は後述します)
ということです。![]() の値が
の値が![]() を超えることもありますが、これはOKです。
を超えることもありますが、これはOKです。
(細かい話をすると、![]() は可積分であるとか、そういうことも必要になります。このあたりになると専門的になるのでここでは省きます)
は可積分であるとか、そういうことも必要になります。このあたりになると専門的になるのでここでは省きます)
確率密度関数から確率を求める
では、この確率密度関数を使って連続量の確率を実際に求めるにはどうすればいいでしょうか?
先程、「コイントス4回」の問題の場合は「2回以上表が出る確率」は起こりうる結果のうち2回以上表が出る結果の割合を、それぞれの確率を足していくことで求めました。
これと同じように、体重が39g以上40g未満の範囲に入る頻度の全体に対する割合を計算すればいいのです。グラフで言うと、(グラフ全体の面積を1とすると)![]() の範囲のグラフの面積が全体に対する割合になりますよね。(この計算がしたかったので、確率密度関数の大事なことに「全体の面積が
の範囲のグラフの面積が全体に対する割合になりますよね。(この計算がしたかったので、確率密度関数の大事なことに「全体の面積が![]() 」が入っていたのでした)
」が入っていたのでした)
ただし、離散の場合は各結果の確率を足していけばよかったのですが、連続な場合はグラフに囲まれた図形の面積を求めるので「確率密度関数の![]() の範囲の定積分」を計算します。つまり、
の範囲の定積分」を計算します。つまり、
![]()
が「インコの真の体重が39g以上40g未満となる確率」です。
「体重が39gである確率が0である」という言葉の意味
最初に話したように連続確率分布の説明をするときには「体重が39gになる確率は0である」という書き方がされていることが多いです。
これは次のように考えます。
先程書いたように、今回は「体重が39gであると計測されたとき、実際の値が39g以上40g未満であることから、その範囲の割合を考える」という考え方をしました。
キッチンスケールの単位を細かくするほど実際の値が入る範囲が狭まります。すると、上のグラフを見ながら考えると「実際の値が入る範囲が狭まるほど全体に対する割合も減っていく」ことが分かります。
体重が39gである、というのは「単位が細かくなるほど、計測した体重が39gに限りなく近くなる」ということを意味します。小数点以下をどんなに計測しても39のあとに出てくる数字が0だけである…というイメージです。
これはつまり、![]() を実際の値の入る範囲としたときに
を実際の値の入る範囲としたときに![]() が
が![]() に限りなく近くなる、ということでもあり、範囲が
に限りなく近くなる、ということでもあり、範囲が![]() に近づくので、全体に対する割合も
に近づくので、全体に対する割合も![]() に近づいていきます。
に近づいていきます。
つまり、「計測の単位を細かくするほど、39gである確率が![]() に近づく」ということが「体重が39gである確率が0である」の言いたいことだと思います。
に近づく」ということが「体重が39gである確率が0である」の言いたいことだと思います。
終わりです。
以上、『確率分布』についての私なりの理解の仕方でした。
前半は数学的事実、後半は「連続な値」に対する私の理解の仕方を中心とした確率の考え方を書いていきました。
以下は感想です。
連続確率分布というのは、個人的には『実際のデータを測る定規』と同じだなと思っています。
実際に得られるデータというのはどんなに頑張っても有限の値でしかなく、それを集めて作った分布(グラフ)も連続関数のような滑らかな形にならないでしょう。
しかし、これが「どのような分布になっているのか」を測るときに使うのが「連続確率分布」のグラフなのかなと考えました。
(実際、計測されたデータを使って「計測した集団の分布が正規分布であるかどうか」を検定する、ということを統計では行ないます)
それで、今回連続確率分布を考えるときに「![]() が1つの値になる確率」でなく、「観測した値が
が1つの値になる確率」でなく、「観測した値が![]() だったとき、観測した時の単位によって決まる実際の値が入る範囲の全体に対する割合」を確率として考える、という捉え方で説明しました。
だったとき、観測した時の単位によって決まる実際の値が入る範囲の全体に対する割合」を確率として考える、という捉え方で説明しました。
個人的に混同していたのが「確率密度関数」と「確率分布」の違いでした。
離散の場合では![]() の値ごとに確率を対応させるので、その関数の連続版が確率密度関数だと思っていたのと、どのようにして確率密度関数が出てくるのか、「確率を足し合わせる」から「積分になる」のが少し不明瞭だったのです。
の値ごとに確率を対応させるので、その関数の連続版が確率密度関数だと思っていたのと、どのようにして確率密度関数が出てくるのか、「確率を足し合わせる」から「積分になる」のが少し不明瞭だったのです。
今回まとめる中で、離散の場合は「![]() に対応する確率」と「
に対応する確率」と「![]() が起こる頻度」が一致していたのですが、連続の場合は「
が起こる頻度」が一致していたのですが、連続の場合は「![]() が起こる(相対的な)頻度」を確率密度関数で表し、「範囲の確率」をその積分として捉えるという対応だったのだと理解できました。
が起こる(相対的な)頻度」を確率密度関数で表し、「範囲の確率」をその積分として捉えるという対応だったのだと理解できました。
最後に、この記事で書いたことを表にしてみたいと思います。
|
離散 | 連続 | |
| 定義 | これ以上細かく計測できないところがある | (理論上)いくらでも細かく計測できる |
| 確率変数に入る値 | 自然数または整数 | 実数 |
| 現象の頻度 | 各結果に確率を対応させる | 確率密度関数で表す |
| 確率の計算 | 各結果の確率を足していく | 範囲の定積分を計算する |
| 確率分布 | 各結果に確率を対応させた関数(頻度と同じ) | 確率密度関数の定積分 |
最初にも書きましたが、今回の説明は数学的事実に基づいて書いていますが、私なりの捉え方も多く書かれています。なので、あくまで理解の参考程度に考えてください。
以上、2日間にわたる日曜数学 Advent Calendar 2021の記事でございました。
前日(12/7)に飛び入り参加、12/8に本日の枠も使うことを決める…という計画性のなさでしたが、tsujimotterさんの温かい対応に本当に感謝します。
また、この記事を読んでくださった皆様に感謝します。
明日は Toshiki Takahashiさんの「世界解決問題と解決エンジン」です。
名前からしてかなり気になる内容なのですが、解決エンジンとはどういうものなのでしょうか…。
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件



