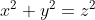とある教室にて、数正、真理、ディーがそれぞれの勉強をしています。
そこにアキがやってきました。
A(アキ)「あー、ディーだ。何してるの?」
D(ディー)「アキか。今授業で統計をやってて宿題してんだ」
X(数正)「ふむ、統計か…」
D「ん、気になるのか?」
X「統計は最近の研究でも使われることがあるからな」
D「ふーん、そうか。
まぁ、俺はAIとかにも興味があるからな」
X「それなら、統計は必須だな」
D「そういうわけで、今も勉強中ってことだ。
…ったく、それにしてもこの分散の計算面倒くさいんだが。
二乗して、足して、![]() で割って…」
で割って…」
M(真理)「…ねぇ」
A「ん、どうしたの?真理ちゃん」
M「どうして分散の計算は『偏差の二乗和』なのかしら?」
A「そういえば、そうだね」
X「ふむ…」
M「…高校の時からずっと気になっていたのよね、これ」
D「分かるぜ。二乗にしなければ計算は簡単なのにな」
X「何言ってるんだ。偏差をそのまま足して、平均を取ると…」
D「![]() になるんだろ。それは知ってるぜ、さすがに」
になるんだろ。それは知ってるぜ、さすがに」
データ![]() の平均値を
の平均値を![]() とすると
とすると
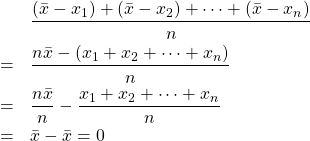
D「こうやって、実際に計算もして確かめた。
なんか変な感じもするが、そうなるんだな」
X「平均はデータの合計を等分したものだからな」
D「…そういうもんか」
A「ちゃんと計算してるんだ!えらいね!」
D「そんな笑顔で言わんでも…なんか恥ずかしいわ。
まぁ、ここで何回もやってきたからな」
M「そこも気にはなるわね…。でも、今は分散の話を考えましょう。
そのまま足せばどのデータでも![]() になるのはその通りだわ。
になるのはその通りだわ。
そうしたら、どうして偏差を二乗するのかしら」
X「…定義に戻るか。
そもそも、分散は何のために考えたんだ?」
D「あー…何だったか?」
M「平均からどのくらいデータの値が離れているのか、分散しているのかを知るための数よね」
D「あ、そうだ、それだ」
X「そうなると、このようなことが成り立ってほしい」
『全てのデータの値が平均に近いならば、分散の値は小さい』
X「さて、一番データと平均が近いのはいつだ?」
D「んー…」
A「えーと…」
M「…全てのデータの値が等しい時、ね。」
A「あ、そっか!」
X「そうだ、全てのデータの値が等しい…それを![]() とするならば、平均値は」
とするならば、平均値は」
D「![]() だな」
だな」
X「となると、このときには当然分散は![]() になる。そして、この逆も成り立ってほしい」
になる。そして、この逆も成り立ってほしい」
D「逆っていうと?」
X「つまり
『分散が![]() に等しいのは、全てのデータの値が等しい時に限る』
に等しいのは、全てのデータの値が等しい時に限る』
ということだ」
M「…!」
X「そして、偏差の二乗和はこれを満たす」
![]() とする。このとき、
とする。このとき、![]() は全て
は全て![]() 以上なので、
以上なので、![]() が成り立つ。
が成り立つ。
M「…分散で考えたいことが満たされるわね!」
X「これが偏差の二乗和を考える理由の一つだ、と思う」
A「へぇ~、ちゃんと理由があるんだ!」
D「…確かに納得はできるが」
X「何が疑問なんだ?」
D「これって、二乗和だけなのか?」
X「…なかなか鋭いな。実際、二乗和以外でもこの性質を満たすものがある。たとえば、偏差の絶対値の和でも成り立つ」
A「あれ、そうなんだ?」
D「そしたら、そっちのほうが計算しやすいだろ」
X「事実、偏差の絶対値の平均は平均偏差と呼ばれるものになる。
一方、分散の平方根は標準偏差と呼ばれる」
D「そしたら、何が違うんだ?」
X「データに対して、最小となる代表値が異なる。
実は平均偏差は”平均値”でなく”中央値”で最小になる。これに対して標準偏差…分散も同様だが、これは”平均値”で最小になるんだ」
この話について、詳しくはこちらを参照ください。
ちゃんと証明がされています。
X「だから、”平均値からどれくらいばらついているのか”を調べるという意味では偏差の二乗和が相応しい」
D「あー、よく考えると『全てのデータの値が等しい』時は平均値だけでなく中央値も最頻値も一緒だからな、そうなるのか」
A「平均偏差は”中央値からどれくらいばらついているのか”を調べるものってことかな?それにしても、あんまり聞かないね…」
X「まぁ、その辺の事情は流石に俺も分からない」
M「…」
D「さっきから、真理は何を計算してるんだ?」
M「偏差の三乗和の平均を計算していたのよ」
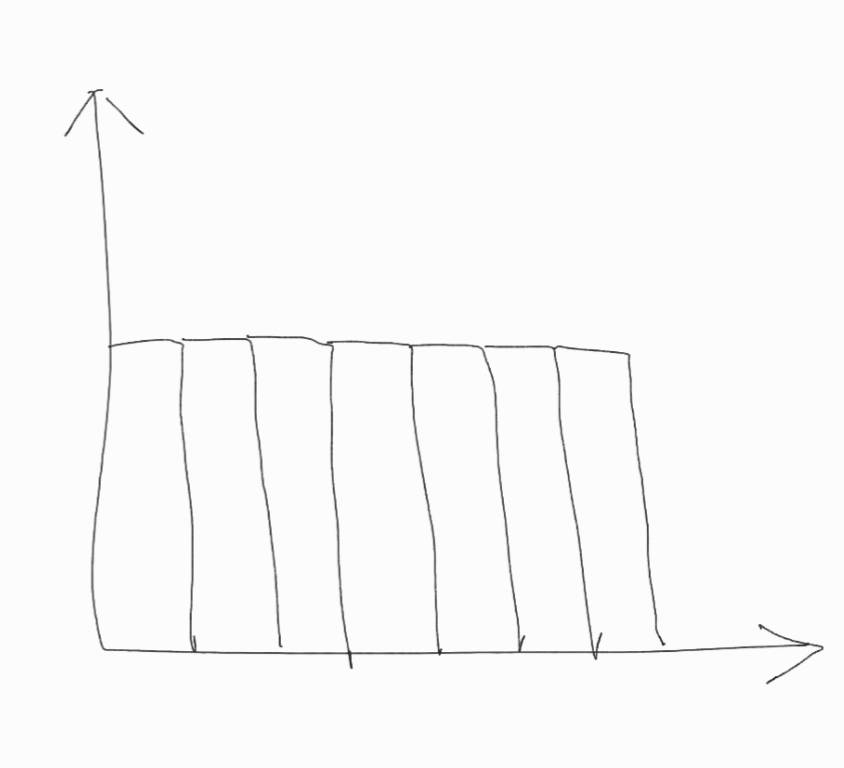
X「三乗和?それだと、先程の条件を満たさないだろう。たとえば…」
X「このようなヒストグラムでも![]() になる。だから、分散の定義には向いていない」
になる。だから、分散の定義には向いていない」
M「…でも、この![]() つはいずれも対称よね?一般に、データが対称ならば、偏差の三乗和は
つはいずれも対称よね?一般に、データが対称ならば、偏差の三乗和は![]() になるわね」
になるわね」
ヒストグラムが左右対称であるとする。このとき、平均値と中央値(と最頻値)は等しく、また、偏差も対称である。ただし、偏差が対称とはデータ![]() に対して(データを小さい順に並べた時)
に対して(データを小さい順に並べた時)![]() が成り立つこととする。
が成り立つこととする。
このとき、![]() が奇数なら平均値と中央値の差は
が奇数なら平均値と中央値の差は![]() になること、
になること、![]() より
より
![]()
が成り立つ。
X「…それは、確かにそうだ」
M「逆に偏差の三乗和が![]() になるのが、対称であるときのみかどうか…はさておいて、これはデータの対称性を表す指標にならないかしら?」
になるのが、対称であるときのみかどうか…はさておいて、これはデータの対称性を表す指標にならないかしら?」
A「…ほぇ~」
D「アキ、さすがに口を開けながら固まるのはどうかと思うぜ」
A「や、ツッコまないでよ、そこは!
だって、真理ちゃんが何を言ってるのかわからないんだもん!」
M「今、私は二乗和だったら分散になるけど、三乗和なら何になるのかを考えてみたのよ。もちろん分散の指標にはならないけど、別の特徴があったというわけ」
X「データが対称である、ということも一つの重要なデータなんだ」
M「この偏差の三乗和の平均を…そうね、対称度…いいえ、ここでは歪んでいる度合い、ということで”歪度”としましょう」
A「歪度…」
M「ところで、データが対称だと何が成り立つかしら?」
D「あー…そういやさっき計算してたな、それ。
中央値が平均値と等しくなるんだったか?」
先程、![]() が奇数の時には成り立つことを書いたが、
が奇数の時には成り立つことを書いたが、![]() のとき、データが対称であることから
のとき、データが対称であることから![]() が成り立つ。よって、中央値は
が成り立つ。よって、中央値は![]() であることに注意して、
であることに注意して、![]() から
から![]() となる。
となる。
M「ええ。それなら、データが対称に近いほど…言い換えると、”歪度”が![]() に近いほど、平均値と中央値が近くなる可能性はあるわね」
に近いほど、平均値と中央値が近くなる可能性はあるわね」
X「ふむ、それは面白そうだ」
A「ねぇねぇ。気になったんだけど、今ヒストグラムって図形が対称なら”歪度”って言ってた数が![]() になるんだよね?それだったら…全然対称になっていない図形なら、”歪度”が大きくなるのかな?」
になるんだよね?それだったら…全然対称になっていない図形なら、”歪度”が大きくなるのかな?」
X「先にそっちを試すか。そうだな…
計算はしやすいようにデータの数は![]() にしたい…
にしたい…
それでいて、明らかに対称とは程遠い…」
D「おーい」
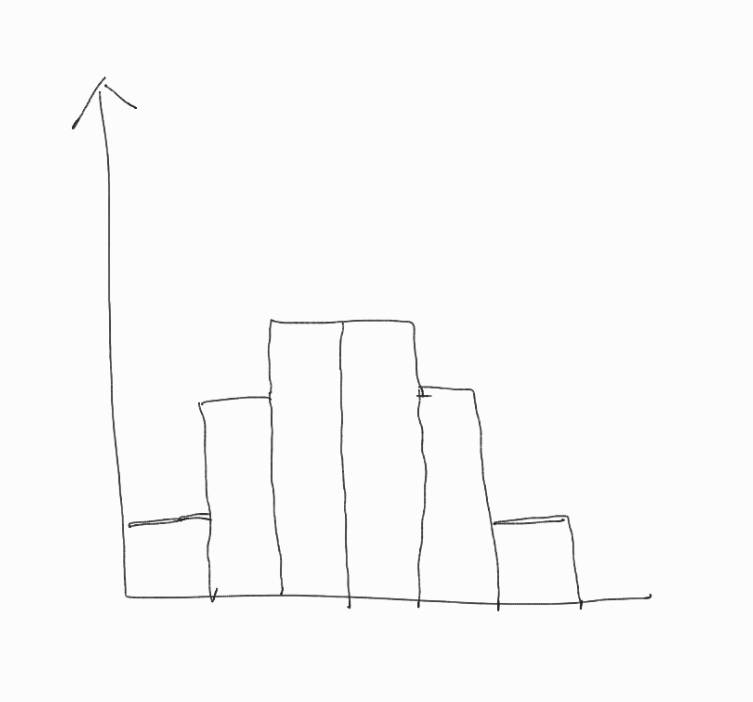
X「よし、それなら。
『![]() が2つ、
が2つ、![]() が3つ、
が3つ、![]() が4つ、
が4つ、![]() が5つ、
が5つ、![]() が6つ』
が6つ』
というものにしよう。これなら平均値も計算しやすい」
D「よし、手始めに中央値だ。これは簡単だな」
A「![]() だね!」
だね!」
D「って、今俺が答えようとしただろ!」
A「ディーは平均値計算してよ!その方が計算の練習になるでしょ?」
D「まじかよ…まぁ、これくらいなら…」
![]()
D「だから、平均値は![]() だな。本当に簡単で良かったぜ…」
だな。本当に簡単で良かったぜ…」
X「まぁ、俺達が暗算でできるくらいのデータにしたからな」
A「この計算暗算でできるんだ!」
M「さて、平均値と中央値の差は![]() ね。これが大きいと見るか小さいと見るかは難しいけど…」
ね。これが大きいと見るか小さいと見るかは難しいけど…」
A「さっきの…”歪度”だっけ?それを計算してみよー!」
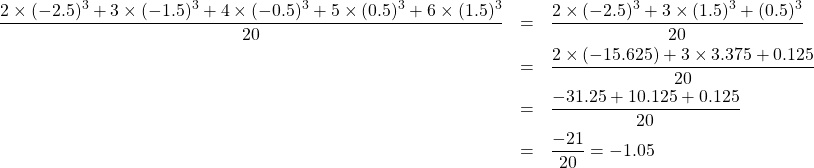
M「へぇ…![]() なのね」
なのね」
X「予想していたより小さい気もするが…中央値より小さい値の方が多いから負なのか?」
M「でも、平均値で比較すると平均値より大きい値の方が多いわね。そうなると、プラスになりそうなものだけど…」
X「![]() という値が大きく離れていることが影響したのか?」
という値が大きく離れていることが影響したのか?」
M「なるほど、改善の必要があるわね…」
A「…すごいな、私ついていけないや」
D「まぁ、ひとまず待とうぜ。ある程度まとまったら教えてくれるだろ」
M「ええ、そうね」
D「って聞いてんのかよ!?」
M「?何を言っているのかしら?」
D「…えっ?」
A「あー…これ、すれ違いのやつかな?
…ま、二人が熱中して話し合っているのを見てるの、私は好きなんだけどねっ」
と、アキが見守りつつ、真理と数正はしばらく議論を続けていました。
その夜。
数正は今日話したことを『教授』にメールで送信していました。
このセミナーを開催する時、真理がお世話になった教授と会い、彼の名義で教室を借りていたのです。
その条件として、セミナーで話したことをまとめて報告するように話していました。彼もまた、数学の面白い話に興味があるのでした。
というわけで、(『教授』からのメールの内容を使って)あとがきです。
ここで”歪度”という言葉が出ましたが、実際この歪度というのは定義がされていまして、実際の定義は![]() を分散の平方根(標準偏差)として
を分散の平方根(標準偏差)として
![Rendered by QuickLaTeX.com \[\frac{1}{n\left(\left(\frac{\bar{x}-x_1}{s}\right)^3+\left(\frac{\bar{x}-x_2}{s}\right)^3+\cdots+\left(\frac{\bar{x}-x_n}{s}\right)^3\right)}\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-1f01f51f592f7953e874e03ed70f7913_l3.png)
となっています。なお、歪度の定義は一つではないようで、また、この定義でも「対称でないデータでも
ちなみに、私はこの話を聞いた時に実際調べて初めて歪度の存在を知りました。
(なお、正式に定義された歪度と区別するため、この文章で真理が定義したものを”歪度”と書きます。)
ところで、最後の例のデータでの”歪度”ですが、本来の定義で計算すると標準偏差が約![]() なので、それを使って計算すると約
なので、それを使って計算すると約![]() となります。なので、小ささはともかくとして、値が負になることには変わりないようです。
となります。なので、小ささはともかくとして、値が負になることには変わりないようです。
ただ、数正が言っていたように![]() という平均値から大きく離れた値が
という平均値から大きく離れた値が![]() つあることが原因なのかもしれません。
つあることが原因なのかもしれません。
偏差の二乗和はデータの数が大きくなるほど大きくなってしまうので、データの数で割って平均を取ったものが分散となります。
これと同じように、偏差を標準化するのに標準偏差を割ったと考えられます。
あと、先程のデータの最後の6つを![]() とすると、平均値は
とすると、平均値は![]() となります。中央値との差は
となります。中央値との差は![]() で先程より小さいです。
で先程より小さいです。
一方、本来の定義の歪度で計算すると![]() と大変小さくなっています。また、正に偏ります。
と大変小さくなっています。また、正に偏ります。
ところが、データの最後の6つを![]() にしてみると、平均値は
にしてみると、平均値は![]() となり中央値との差は
となり中央値との差は![]() になる一方、歪度は
になる一方、歪度は![]() くらいとなり、離れてしまいました。このことから『中央値と平均値の差』というのは歪度とは関係なさそうなものだと考えられます。また、ヒストグラムが対称でないのに小さくなったのも疑問です。
くらいとなり、離れてしまいました。このことから『中央値と平均値の差』というのは歪度とは関係なさそうなものだと考えられます。また、ヒストグラムが対称でないのに小さくなったのも疑問です。
歪度がかなり小さくなるところがあったことから、何かしらのバランスが関係しているのかな、と個人的には予想しています。
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件