【数学小説】真理の森の数学セミナー～積分編⑦～

SHARE

→積分編⑥

「確かにこの面積の求め方は直感的には正しそうだけど、よくよく考えると”一つ一つのパーツの面積が0になる”という問題があるわ。
そこで…もう少し深く考えましょう」

そう話して、真理は黒板に図に幾つか線を追加しました。

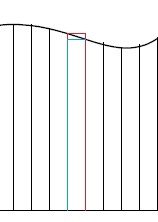
「今、2つの長方形を書いたわ。
このうち赤いほうは”区間内で最も大きい値”を高さとした長方形。
青いほうは”区間内で最も小さい値”を高さとした長方形よ」

「2つの長方形の間にグラフのパーツがある、ってことは…
パーツの面積は2つの長方形の面積の間、ってこと？」

「そうよ。今、このパーツの面積をS_k、区間の長さを\epsilon_kとしましょう。
青い方の高さをf(a_k)、赤い方の高さをf(b_k)とすると…」

「え、ちょっと待って！？」

と、ここでアキが少し慌てて止めました。

「なんだか、色々な文字がたくさん出てきて混乱しそう…」

「それもそうね。一つ一つ説明するわ」

「うん、まず…パーツの面積をS_kってしているけど、”k”って何？」

「あぁ…これはもう少し後で分かるのだけど、k番目のパーツの面積という意味なのよ」

「k番目…？」

「ええ。今、この面積は幾つかのパーツに分けられているのだけど、そのある一つを取ったのよ。それが”k番目”ってこと」

「…」

アキはまだモヤモヤしている様子です。

「たとえば、最初のパーツは1番目だから面積がS_1になるの」

「あ、そういうことか！そしたら2番目のパーツの面積はS_2ってこと？」

「それでいいわ。
このパーツは何番目の数か分からないから、kって置いているの。
実際にはS_1,\ S_2,\ldotsと続くの」

「ふむふむ。なんとなく分かってきた！
…でも、直接数えたら何番目か分かるんじゃないかな？」

「フフフ…その発想は面白いわね」

真理は微笑みながら、話を続けました。

「でも、ここではk番目の話について設定するのが大事なのよ。それはもう少し後に分かるわ。
それと…」

それから悪戯っ子のような笑みを浮かべて話しました。

「仮に100000位細かく切ったとして、このパーツは何番目って数えるのは大変じゃない？」

「……うわぁ…」

真理の言葉を想像して少しゲンナリしたアキ。

「だから、k番目って数字を置いて、何番目のパーツでもいいようにしているのよ」

「うん、なんか文字で置いた方がいい気がしてきた…」

「慣れないと難しいのだけど、慣れればこれほど便利なものはないわね。
さて、続けましょう。\epsilon_kは…」

「”k番目の区間の長さ”ってこと？」

「ええ。慣れるのが早いわね」

「まぁ、さすがに何回かサークルで勉強したからね！」

アキは喜んでそう話しました。

「それでは、次にf(a_k)とf(b_k)だけど、これはこの区間における最小値と最大値のことよ」

これについて、アキでなくディーが答えました。

「…つまり、f(x)はa_kのときに最も小さくて、b_kのときに最も大きい、ってことか？」

「筋が良いわね」

「まーな！」

真理に褒められ得意気なディーです。

「でも、ちょっと惜しいわ。
このa_kやb_kは”k番目の区間で”最小・最大のところよ。全体では最小・最大とは限らない」

「あ…いや、それは分かってたんだが、言葉が抜けてたんだ！」

「フフ…」

慌てて取り繕うディーに思わず笑ってしまう真理。

「では、文字については説明したところで、続けましょう。
このパーツの面積をS_k、区間の長さを\epsilon_k、青い方の高さをf(a_k)、赤い方の高さをf(b_k)とすると…」

    \[f(a_k)\epsilon_k \le S_k \le f(b_k)\epsilon_k\]

「このような式が成り立つわ」

「…青い方の面積がf(a_k)\times\epsilon_k、赤い方はf(b_k)\times\epsilon_kだから…確かにこうなるな」

「そして、今区間をn等分したとして、各区間ごとのそれぞれの面積を足し合わせると…」

    \[\sum_{k=1}^n f(a_k)\epsilon_k \le \sum_{k=1}^n S_k \le \sum_{k=1}^n f(b_k)\epsilon_k\]

「このようになる。真ん中の式は…」

「それぞれのパーツを足し合わせたから、求めたい図形の面積だ！」

「その通りよ。これをSとしましょう。すると、このような等式が成り立つ」

    \[\sum_{k=1}^n f(a_k)\epsilon_k \le S \le \sum_{k=1}^n f(b_k)\epsilon_k\]

「求めたい面積を2つの長方形の和、という分かっている図形の面積で近似した、ということだ」

と数正が補足しました。

「さて、ここからがちょっと難しい話なのだけど…。
今の数式を図で説明すると、このような形になるわ」

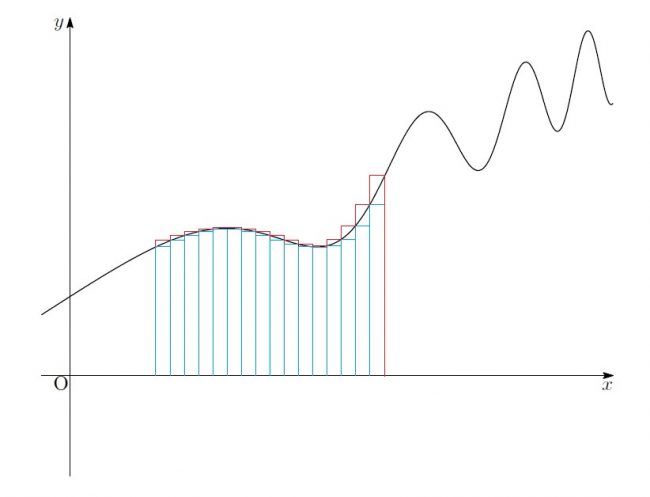
「青が小さい方の長方形、赤が大きい方の長方形を足し合わせたものになるわ。
そして、この図形とグラフの隙間が”Sとの差”になる。
この差が…”区間を細かく分けるほど小さくなる”なら、Sと青い図形の面積の”極限”が一致するはずよね」

「…極限」

その言葉を聞いて若干真剣な顔で考えるアキ。

「区間をn等分したときの青い方の面積をL_n、赤い方の面積をM_nとすると…」

    \[L_n=\sum_{k=1}^n f(a_k)\epsilon_k,\ M_n=\sum_{k=1}^n f(b_k)\epsilon_k\]

「nを限りなく大きくする、言い換えると限りなく細かく区間を分けたとき、L_nとM_nが収束して極限値が一致したとき…」

    \[\lim_{n\rightarrow \infty}L_n=\lim_{n\rightarrow \infty}M_n\]

「この極限値はSと一致する」

    \[S=\lim_{n\rightarrow \infty}L_n\]

「つまり、これが積分の”定義”になるのよ。この定義の方法を…数正は名前知っているわよね？」

「ああ…」

真理に振られて、数正はその名前を話しました。

「”区分求積法”だな」

→積分編⑧

→まとめへ戻る

この記事を書いたブロガー

sato
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

前の記事

【数学小説】真理の森の数学セミナー～積分編⑥～

次の記事

Galaxy Note8がかなり絵を描くのに良い件について