〈1/27更新数式の間違いを修正しました〉
<1/31編集 スマホに合わせて一部数式のサイズを変更しました。何故か数式の最後に番号が付いていますが、これについては現在解決策を検索中です…。>
→積分編①
数正は黒板の前に立つと、![]() 公式を書き出しました。
公式を書き出しました。
![]()
「これは、一度展開して計算すればいい。多項式の積分だから、アキも習っているはずだ」
「う、うん…一つ質問いいかな?」
「もちろん」
アキはおずおずと手を挙げて質問します。
このセミナーにはいくつか決めごとがあって、その一つが
「どんなに”当たり前に思える”ようなことでも質問していい」
です。
「この”![]() ”や”
”や”![]() ”って何?」
”って何?」
アキが質問しているのは、この公式に出てくる”![]() ”や”
”や”![]() ”のことについてです。
”のことについてです。
「あ、これか。
これは数だ」
「数、ってことは”1″とか”2″とかってこと?」
「あぁ。もちろん”-1″でも”![]() ”でも”
”でも”![]() ”でもいい。実数ならなんでも」
”でもいい。実数ならなんでも」
「そうなんだ…」
「もっと言うと、この”![]() ”や”
”や”![]() ”は『積分の中身の方程式の解』になっている」
”は『積分の中身の方程式の解』になっている」
「…」
むーっという表情でしばらく黒板の式を見ていたアキですが、
「あ、そっか」
といってノートに計算を書きました。
![]()
「確かにそうだね」
それを横で見た真理が一言話します。
「単純に代入すればいいわ。片方が0になるから方程式の解になることが分かる」
![]()
「あ、ホントだ!」
真理の言葉に納得したアキ。
続けて、真理は数正に突っ込みます。
「それから、『積分の中身の方程式』は違うわね。
積分の中にあるのは『2次関数』だから、『積分の中の2次関数が0になる数』の方がいいわ。
本当は”2次関数の零点”というのが一番スッキリするのだけど」
「…そうだな。間違ってた。
そういうわけで、真理が話していた”零点”という言葉を借りると…この左辺の式は
“ある2次関数が2つの異なる実数の零点を持つ時、その2次関数を一つの零点からもう一つの零点までの間で積分する”
ということを表している」
「零点というのは![]() を満たす
を満たす![]() のことよ。
のことよ。
今の場合”異なる2つの実数解を持つ2次方程式”の解、つまり![]() と
と![]() というわけ」
というわけ」
零点、という聞きなれない言葉について真理が補足して説明しました。
「ふーん、そういう意味だったんだな…」
数正の言葉を頭に浮かべながら、なるほどと思うディー。
「ねぇ、それって、『異なる2つの実数解を持つ』2次方程式でないとダメなの?」
とアキは再び質問してきます。
「?どういうことだ?」
「んー、だからね。
この2次関数は『異なる2つの実数解』…じゃなくて…えと、2つの零点を持つんだよね?
それって『異なる2つの実数』だけじゃないとダメなのかな?って」
それに、横にいる真理が答えます。
「それは、この式の”図形的”な意味を考えると分かり易いわ。
2次方程式が2つの異なる実数解を持つということは『放物線が![]() 軸と異なる2点で交わる』ということでもあるのよ」
軸と異なる2点で交わる』ということでもあるのよ」
「えと…2次関数のグラフって放物線だっけ?」
「えぇ。積分の中身![]() が表す2次関数
が表す2次関数![]() はこんなグラフになるわ」
はこんなグラフになるわ」
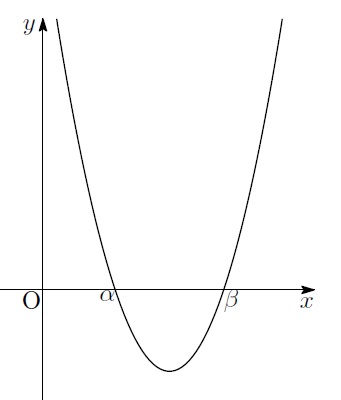
「…![]() は
は![]() になって放物線、
になって放物線、![]() 軸との交点は…」
軸との交点は…」
「![]() 軸は
軸は![]() だから、
だから、![]() の解、つまり
の解、つまり![]() になる」
になる」
「…うん、おっけーだよ」
なんとかこの話を飲み込めたアキ。
「でね、左辺はこの放物線の…」
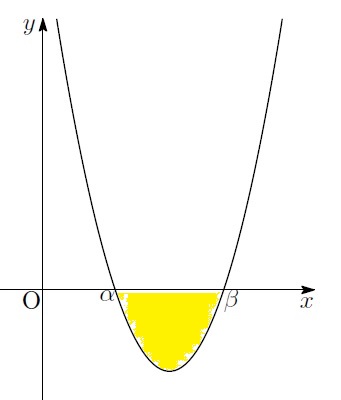
「この部分の面積を表しているの」
「うん、確か定積分…ニョロニョロ![]() のところに数が置かれているものはグラフのそこからそこまでの面積に…」
のところに数が置かれているものはグラフのそこからそこまでの面積に…」
「いや、ニョロニョロってなんだよ!」
思わずディーが突っ込んでしまいます。
「いや、ニョロニョロってしてるから…何ていうんだっけ?あの記号」
「”インテグラル”だ。積分を英語で言うとintegralになる。
それから、インテグラルの下の方に付いている![]() が区間の始め、
が区間の始め、![]() が区間の終わりを表す。
が区間の終わりを表す。
だから、この積分は”![]() から
から![]() までのグラフと
までのグラフと![]() 軸で囲まれた面積”を表しているんだ」
軸で囲まれた面積”を表しているんだ」
「![]() のとき、つまり2次方程式が重解を持っている場合は…放物線がこうなるの」
のとき、つまり2次方程式が重解を持っている場合は…放物線がこうなるの」
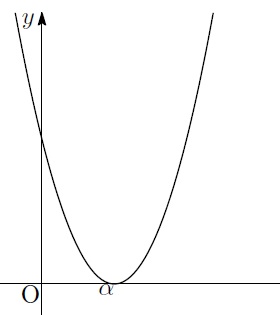
数正の言葉を継いで、真理が説明します。
「あ、グラフで囲まれたところがなくなってる!」
「だから、異なる実数解にしているの。もっとも、この場合でも定積分は定義できるわね。この場合は0よ」
![]()
「そうか、そうしたらこの公式は![]() でも成り立つのか」
でも成り立つのか」
「右辺は
![]()
だから、確かにそうだな。…って、これ公式使わなくてもいいじゃないか!」
「まぁ、そうね。
だけど、この公式がどこまで成り立つのかを知ることは大事よ」
ディーのツッコミに真理が返したところで、アキが再び手を挙げて質問します。
「一応聞くけど…方程式の解がない場合ってどうなるの?」
「実数解がない場合ね。
その場合、グラフはこうなるわ」
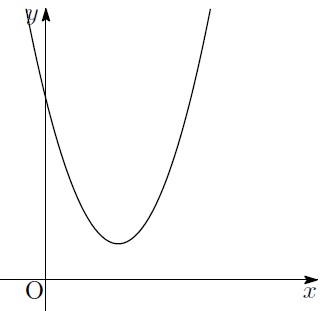
「あ、そもそも交点がないんだ。じゃあ、公式使えないね」
アキは納得したようにうなずきました。
「さて、そろそろ左辺の式の意味は見えてきたかな?」
「うん、初めよりは納得できた!」
数正の問いに笑顔で答えるアキです。
アキは他の三人と違って文系なので、数学にそこまで慣れていません。
だけど、サークルの方針の一つである
「分からない人にも伝わるように教えることを心掛ける」
という決まりのお陰で少しずつ数学を理解していっています。
「よし、そうしたら計算してみよう。
この式は覚えているか?」
![]()
「うん、これは大丈夫!」
「じゃあ、これを使っていく。最初に積分の中を展開して…」
「せっかくだから、ディーが計算したら?」
と、真理が提案しました。
「いや、ちょっと待てよ!なんで俺が…」
「あ、それいい!ディーはもっと計算して数学を得意にならないと!」
ディーは嫌そうにしていましたが、アキは喜々として計算することを推していました。
「確かにそうだな。ちょうど積分を授業でしているし…」
「マジかよ…まったく…」
「大丈夫、規則通りに計算すればいいだけだ」
「ホントかよ…とりあえずやるぞ」
そういって、ディーが黒板に計算を書いていきました。
![Rendered by QuickLaTeX.com \begin{eqnarray*}{{\footnotesize&&\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\\&=&\int_{\alpha}^{\beta}(x^2-(\alpha+\beta)x+\alpha\beta)dx \\&=&\left[\frac{1}{3}x^3-\frac{1}{2}(\alpha+\beta)x^2+\alpha\beta x\right]_{\alpha}^{\beta}\\&=&\frac{1}{3}(\beta^3-\alpha^3)-\frac{1}{2}(\alpha+\beta)(\beta^2-\alpha^2)+\alpha\beta (\beta-\alpha)\\&=&\cdots}\end{eqnarray*}](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-833ce09b1b5f44aa3581a860035f6b36_l3.png)
「って、めんどくせぇことになってるじゃねぇか!?」
「いいからいいから…」
「はぁ、とりあえず展開するぞ…」
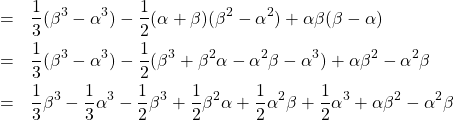
「同じような文字が出てきたな…それにしても本当に合ってるのかね…」
「いや、真ん中の辺りが間違ってる。![]() のところだけ、符号が逆になっていない」
のところだけ、符号が逆になっていない」
「…あー、ホントだ。
こういうグチャグチャした計算本当に嫌だわ…」
「こういうときは同じ項同士で計算するといいわね。そのほうが見やすいし」
「そうだな」
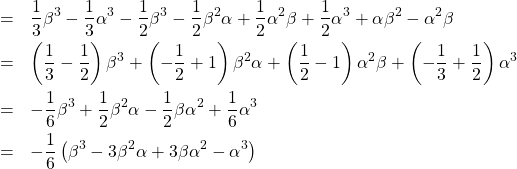
「あ、カッコの中身3乗公式だ!」
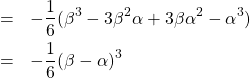
「…はぁ、はぁ…や、やっっと終わった!」
「お疲れさまー!」
「思ったより複雑だったな…」
計算してヘトヘトのディーをねぎらうアキ。
数正は一連の計算を見ながらつぶやきました。
「いや、自分で計算してからやれよ!」
「いや、俺はもう少し簡単な方法を考えていたからな」
「へっ?」
数正の言葉に驚くディー。
![Rendered by QuickLaTeX.com \begin{eqnarray*}&&\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\\&=&\int_{\alpha}^{\beta}(x^2-(\alpha+\beta)x+\alpha\beta)dx \\&=&\left[\frac{1}{3}x^3-\frac{1}{2}(\alpha+\beta)x^2+\alpha\beta x\right]_{\alpha}^{\beta}\\&=&\cdots\end{eqnarray*}](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-0f99c5652ccffdd61247c18bc003f8e8_l3.png)
「このあと、![]() の中身をこうする」
の中身をこうする」
![Rendered by QuickLaTeX.com \begin{eqnarray*}{{\footnotesize&=&\left[\frac{1}{3}x^3-\frac{1}{2}(\alpha+\beta)x^2+\alpha\beta x\right]_{\alpha}^{\beta}\\&=&\left[x^3-(\alpha+\beta)x^2+\alpha\beta x-\left(\frac{2}{3}x^3-\frac{1}{2}(\alpha+\beta)x^2\right)\right]_{\alpha}^{\beta}}\end{eqnarray*}](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-9e3c810e5fdfebe9e9c3c94ce448e459_l3.png)
「え、これって大丈夫なの?」
「ああ。ちゃんと計算したら元に戻るだろう?」
アキは自分のノートで計算して、確かめてみました。
「…うん、確かに戻る。でもどうしてこうするの?」
「さっきの![]() を使いたいから。これは
を使いたいから。これは![]() や
や![]() を代入したら0になるだろう?
を代入したら0になるだろう?
それで計算を少し楽にするのさ」
「最初の項は![]() って因数分解できるから、今数正が話したことを使えるってわけ。
って因数分解できるから、今数正が話したことを使えるってわけ。
こうやって似たような形の式が出てきたら、最初に出た式に変形するのは計算の工夫の一つね」
と、真理が付け加えました。
「計算を続けよう」
![Rendered by QuickLaTeX.com \begin{eqnarray*}{\footnotesize&=&\left[x^3-(\alpha+\beta)x^2+\alpha\beta x-\left(\frac{2}{3}x^3-\frac{1}{2}(\alpha+\beta)x^2\right)\right]_{\alpha}^{\beta}\\&=&-\frac{2}{3}\beta^3+\frac{2}{3}\alpha^3+\frac{1}{2}(\alpha+\beta)(\beta^2-\alpha^2) \\&=&-\frac{2}{3}\beta^3+\frac{2}{3}\alpha^3+\frac{1}{2}\alpha\beta^2-\frac{1}{2}\alpha^3+\frac{1}{2}\beta^3-\frac{1}{2}\beta\alpha^2\\&=&\left(-\frac{2}{3}+\frac{1}{2}\right)\beta^3+\left(\frac{2}{3}-\frac{1}{2}\right)\alpha^3+\frac{1}{2}\alpha\beta^2-\frac{1}{2}\beta\alpha^2\\&=&-\frac{1}{6}\beta^3+\frac{1}{2}\alpha\beta^2-\frac{1}{2}\alpha^2\beta+\frac{1}{6}\alpha^3\\&=&-\frac{1}{6}\left(\beta^3-3\alpha\beta^2+3\alpha^2\beta-\alpha^3\right)\\&=&-\frac{1}{6}(\beta-\alpha)^3}\end{eqnarray*}](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-aef44d00c5ecf5a1e627bd43244d675d_l3.png)
「こうなる。最後の方はちょっと大変だが、少し計算が楽になった」
「先に教えてくれよ…」
恨めしく数正を見ながらつぶやくディー。
「まぁまぁ。こうやって計算するのが大事だっていつも真理ちゃんが話しているじゃん!」
「そ、そうね」
アキの言葉にちょっと動揺して話す真理。
実は「真理ちゃん」と呼ばれるのに慣れてないので、それに動揺していたのでした。
「確かに…式の形を意識するのが大事だっていうことは分かったわ…宿題する時にも意識するぜ」
「まぁ、計算は大変だが、これで”![]() 公式”が成り立つことが示された」
公式”が成り立つことが示された」
そういって、数正が公式の証明を締めくくりました。
「って、大事なところ俺がやってるんじゃねぇか!?なんで数正が締めくくるんだ!」
「…確かにおかしいな…」
ディーのツッコミに首をかしげる数正。
「まぁ、いいか。”![]() 公式”が正しいことは…」
公式”が正しいことは…」
「…気持ち悪いわね」
と、その時、真理が一言つぶやきました。
→積分編③
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件

