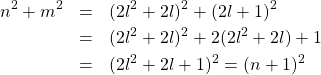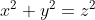目次 非表示
まえがき
おはようございます、satoです。
こちらの記事は日曜数学 Advent Calendar 2020の13日目の記事になります。
カレンダーを企画してくださったtsujimotterさんに感謝です。
というわけで、久々の数学小説です。お題目は【原始ピタゴラス数】。今回はSS形式で書いていこうと思います。
M→真理、X→数正、A→アキ、D→ディーです。詳しい設定等はこちらを御覧ください。
初見の方も多いかもなので、簡単に話すと「数学に興味のある大学生4人が数学の問題についてあれこれ自由に考える」物語です。真理、数正が数学が得意(数学科の学生)、アキ、ディーはそこまで得意でない、感じの設定です。
…本編を書くためのリハビリも兼ねているのはここだけの話です(^_^;)
前文:フェルマーの最終定理
ある日の夕方。
数正、アキ、ディーの三人はいつもの活動のために集まっていました。
と、そこに何やら上機嫌の真理がやってきました。
M「ふふ…やはり『数学ガール』は面白くていいわね」
A「あ、真理ちゃんだ。どうしたの、そんなニコニコして」
M「…そんなに笑っていたかしら?
『数学ガール』フェルマーの最終定理を読んでてとても面白かったのよ」
A「フェルマーの最終定理?」
M「こういう問題よ」
といって、黒板に真理は一つの数式を書きました。
を
以上の自然数とする。このとき、
を満たす自然数は存在しない。
二人の会話するところを見ていたディーと数正が話し出しました。
D「…なんだ、この式。めっちゃ難しいじゃねぇか」
X「…そうか?」
D「数正みてーな数学が得意なやつなら簡単なんだろーけどよ。
数学が苦手な俺なんかにはさっぱりだぜ」
M「具体的には?」
D「文字がいっぱいありすぎて、ちんぷんかんぷんだ」
そういって、両手を挙げるディー。
X「数学に出てくる文字が何を表しているのかを一つずつじっくり見ていけばいい。
最初の![]() は”
は”![]() 以上の自然数”って書いてある」
以上の自然数”って書いてある」
D「じゃあ、![]() って具体的にはなんなんだよ」
って具体的にはなんなんだよ」
X「![]() 以上の自然数なら何でもいい。
以上の自然数なら何でもいい。![]() でも、
でも、![]() でも…」
でも…」
M「そもそも、この数式は無数にあるものをまとめて書いているわ。
たとえば、![]() を
を![]() とすると、
とすると、![]() という式が出てくる」
という式が出てくる」
A「![]() なら
なら![]() ってこと?」
ってこと?」
M「ええ。そして、その一つ一つに対して等式を満たすような自然数![]() が存在しないって主張しているわ。これがフェルマーの最終定理よ」
が存在しないって主張しているわ。これがフェルマーの最終定理よ」
D「…ってことはなにか?たとえば![]() が
が![]() なら
なら
![]()
を満たす自然数
X「そうなるな。そしてそれが…」
A「ちょっとまった!
その、存在しない…ってどういう感じなんだろ?なんとな~くはわかるんだけど…」
X「![]() には自然数がそれぞれ入る」
には自然数がそれぞれ入る」
A「自然数って![]() のことだったっけ?」
のことだったっけ?」
X「そうだ。そして、![]() をどのような自然数にしても、
をどのような自然数にしても、![]() は
は![]() にならない、というのが主張だ」
にならない、というのが主張だ」
M「…もう少し噛み砕いて言うなら、
”2つの自然数の3乗の和はある自然数の3乗にならない”
という言い方になるかしら」
A「…うん。さっきよりは意味が分かってきた気がする。
たとえば、![]() を計算すると
を計算すると![]() になって…これは
になって…これは![]() が
が![]() で
で![]() が
が![]() だから…確かに自然数の3乗にならない。
だから…確かに自然数の3乗にならない。![]() がどんな2つの自然数でも、同じように自然数の3乗にならないってことかな?」
がどんな2つの自然数でも、同じように自然数の3乗にならないってことかな?」
と、黒板に計算しながらアキが数正の方を向いて話しました。
X「それで合っている」
A「やったー!」
D「アキが具体的な数字で書いたから、俺も理解できたわ。で、これが![]() でも成り立つってことか?」
でも成り立つってことか?」
M「![]() だけでなく、
だけでなく、![]() でも
でも![]() でも成り立つのよ。
でも成り立つのよ。
”2つの自然数の![]() 乗の和は、自然数の
乗の和は、自然数の![]() 乗にならない”
乗にならない”
”2つの自然数の![]() 乗の和は、自然数の
乗の和は、自然数の![]() 乗にならない”…という命題が無数にあって、それらがすべて正しい、としている」
乗にならない”…という命題が無数にあって、それらがすべて正しい、としている」
D「はー…なんか難しそうだな」
A「ん?どういうこと?」
D「だってよ、自然数の3乗になる数って無数にあるんだろ?その中には一個くらい2つの自然数の3乗の和で表されるものがあるかもしれないじゃねぇか。
それが一個もない、というのを確かめるのが難しそうだなって思うだろ」
M「…その感覚は正しいわね。
実際、”2つの自然数の3乗の和はある自然数の3乗にならない”という問題は公開されてからおおよそ100年後に正しいことが示されたわ」
A「100年後!?」
D「マジか…」
X「証明したのはオイラーだな。
それに加えて、実際にはすべての![]() 以上の自然数で
以上の自然数で
”2つの自然数の![]() 乗の和はある自然数の
乗の和はある自然数の![]() 乗にならない”
乗にならない”
ということを示さなければならないわけだ。最終的に問題が知られてから330年後にようやく正しいことが証明された」
M「証明したのはアンドリュー・ワイルズ。その証明は代数幾何学、数論、群論、可換環論、モジュラー関数…などなど、現代数学の最先端の技術が使われたとても面白いものになっているわ」
早く読めるようになりたいわね…と喜悦の表情で小さくつぶやく真理です。
その姿は美味しいご飯を前にしている人のよう。
原始ピタゴラス数
X「『数学ガール』にその話があったのか?」
と、来たときの真理の表情を思い出しながら、数正は言いました。
M「さすがにフェルマーの最終定理の証明について詳しくは書かれていないわ。
でも、面白いところは色々あった。たとえば、原始ピタゴラス数が無数に存在することの証明ね」
A「原始ピタゴラス数…?」
D「ってなんだよ?」
X「まず、ピタゴラス数というのは、次の等式を満たす3つの自然数![]() の組のことを言う」
の組のことを言う」
A「あれ、これってピタゴラスの定理?」
X「そう、三平方の定理とも言うな。
これが成り立つような自然数の組がピタゴラス数だ」
D「これ、さっきの式に似ているな」
M「フェルマーの最終定理はピタゴラスの定理…もしくは三平方の定理が元になっているわ。似ているのはある意味当然ね」
A「![]() が一つ違うだけで等式が成り立つ自然数が存在しなくなるんだね…」
が一つ違うだけで等式が成り立つ自然数が存在しなくなるんだね…」
X「そこが数学の面白いところと言える。![]() を変えるだけで、無数に存在するか、そうでないかが大きく変わる。それがどうしてかを突き詰めるのが、フェルマーの最終定理に繋がったわけだ」
を変えるだけで、無数に存在するか、そうでないかが大きく変わる。それがどうしてかを突き詰めるのが、フェルマーの最終定理に繋がったわけだ」
M「具体的な例は分かるかしら?」
D「そうだな…こんなのあったよな?」
![]()
A「えっと、左辺は![]() で右辺も
で右辺も![]() だから確かに成り立つね。
だから確かに成り立つね。
すごーい!よく覚えてたね」
D「これは何故かたくさん見たからな」
X「今、![]() という自然数の組はピタゴラスの定理を満たすことが分かった。実は一つ自然数の組を見つけたら、それらをすべて
という自然数の組はピタゴラスの定理を満たすことが分かった。実は一つ自然数の組を見つけたら、それらをすべて![]() 倍したものもピタゴラスの定理を満たす」
倍したものもピタゴラスの定理を満たす」
A「そうなの?試しに、![]() を
を![]() として、2倍してみようっと。
として、2倍してみようっと。
えっと、![]() で…」
で…」
D「足したら![]() 、これは
、これは![]() の2乗だな」
の2乗だな」
A「あっ!![]() はちゃんと
はちゃんと![]() の2倍だ!」
の2倍だ!」
M「![]() 倍したものは次のように成り立つことが分かるわ」
倍したものは次のように成り立つことが分かるわ」
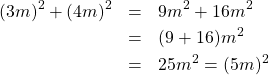
A「2つとも![]() 倍しているから、
倍しているから、![]() で括れるんだね」
で括れるんだね」
X「このように、一つピタゴラス数を見つければ、![]() 倍することで無数にピタゴラス数が見つけられる。
倍することで無数にピタゴラス数が見つけられる。
しかし、せっかくなら![]() の
の![]() 倍したもの以外にピタゴラス数があるかどうかを考えたい。そこで出てきたのが原始ピタゴラス数だ」
倍したもの以外にピタゴラス数があるかどうかを考えたい。そこで出てきたのが原始ピタゴラス数だ」
D「ようやく原始ピタゴラス数のおでましってわけか」
X「原始ピタゴラス数というのはピタゴラス数![]() で互いに素なものを言う。互いに素、というのはなにか分かるか?」
で互いに素なものを言う。互いに素、というのはなにか分かるか?」
D「…わからん」
X「![]() という3つの自然数の最大公約数が
という3つの自然数の最大公約数が![]() になるということだ。
になるということだ。
別の言い方をすると、3つの数すべてを割り切るような![]() 以上の自然数が存在しない、ということでもある」
以上の自然数が存在しない、ということでもある」
M「たとえば、![]() は原始ピタゴラス数になっているわね。ディー、確認してみて」
は原始ピタゴラス数になっているわね。ディー、確認してみて」
D「あー…公約数ってどうやって求めるんだっけか?」
A「ひとまず、約数を考えてみたらいいんじゃない?」
D「![]() の約数は
の約数は![]() で
で![]() の約数は
の約数は![]() 、
、![]() の約数が
の約数が![]() で…。
で…。
全てに出てくるのが公約数だったな!思い出したぜ!
今の場合は![]() しかない、だから互いに素、ってわけか」
しかない、だから互いに素、ってわけか」
X「![]() はピタゴラスの定理を満たすことはさっき確認したから、これで原始ピタゴラス数であることが示された」
はピタゴラスの定理を満たすことはさっき確認したから、これで原始ピタゴラス数であることが示された」
A「うん、分かった感じがする!それで、これはどれくらいあるの?」
M「私が話したかったのはそこ。
この原始ピタゴラス数は無数に存在するのだけど、その証明のあらましを最後にユーリちゃんが出したのよ」
A「”ユーリちゃん”って?」
M「『数学ガール』に出てくる人物の名前。中学生だけど、高校生の主人公たちと一緒に数学を勉強するのよ。
面白かったのはその証明ね」
D「どんななんだ?」
M「まず、連続する2つの自然数を取ってくる。小さい方を![]() とすると、
とすると、![]() となるわ。そして、この
となるわ。そして、この![]() つの自然数の差を取るの。すると、次のような式が成り立つわ」
つの自然数の差を取るの。すると、次のような式が成り立つわ」
D「ふーん、なんかうまく整理された感じがするが…」
A「ん?これってどこかで見た気がするような?」
D「これ、って?」
A「最後の式。えーっと…
そうだ!奇数ってこうやって表されなかったっけ?」
M「その通り、2つの連続する自然数の2乗の差は必ず奇数になる。しかも、![]() は任意の自然数だから、
は任意の自然数だから、![]() はすべての奇数になる。
はすべての奇数になる。
あとは、![]() をある奇数
をある奇数![]() の
の![]() 乗にすれば、
乗にすれば、![]() とこの奇数
とこの奇数![]() は原始ピタゴラス数になる。
は原始ピタゴラス数になる。![]() が奇数の2乗となるような
が奇数の2乗となるような![]() は無数に存在するから、原始ピタゴラス数は無数に存在する、というわけね」
は無数に存在するから、原始ピタゴラス数は無数に存在する、というわけね」
X「ふむ、せっかくだから、もう少ししっかり詰めるとしよう。
奇数の2乗から考えるのがよさそうか…![]() を奇数としよう。つまりこうだな」
を奇数としよう。つまりこうだな」
X「![]() は任意の自然数。すると」
は任意の自然数。すると」
X「このように変形されるから、![]() とすればいい。あとは…」
とすればいい。あとは…」
X「こうなって、確かにピタゴラスの定理が成り立つことが示された」
D「…わけわからん。一体何をしたんだ?」
X「さっきの真理の説明を聞いて、具体的に![]() が奇数の2乗となるような
が奇数の2乗となるような![]() を求めたかった。だから、あらかじめ奇数を一つ取ってきて、そこから
を求めたかった。だから、あらかじめ奇数を一つ取ってきて、そこから![]() を求めたんだ。
を求めたんだ。
その後、![]() がピタゴラス数であることを証明した」
がピタゴラス数であることを証明した」
A「ふむふむ。じゃあ、最後の変形は?」
X「示したかったのは![]() となることだからな。
となることだからな。
そのように因数分解をしたかった。
幸い、![]() を求める時に同じ式変形をしたから、見やすくなったんだ」
を求める時に同じ式変形をしたから、見やすくなったんだ」
A「…ホントだ!書いてあった!」
D「それで、ピタゴラス数であることを確かめたってわけか。
あれ、でもよ。これって本当に互いに素なのか?」
X「そこに気づくとは、なかなか鋭いな」
D「まぁ、俺もここでだいぶ勉強したからな」
へへっ、と気分良さげなディーです。
X「まず、![]() と
と![]() が互いに素なのは…」
が互いに素なのは…」
M「せっかくだから、これもちゃんと示しましょう。
あとの役に立つわ」
と、真理が口を挟みました。
X「ふむ、珍しいな、いつもはこういうのは飛ばすことが多い気がしたが…」
M「私が考えた問題の話にも繋がるのよ」
X「そうか…では、示そう。
互いに素であることを確かめるときには、公約数を![]() として、
として、![]() となることを示すことが多い。今回もそのようにする。
となることを示すことが多い。今回もそのようにする。
今、![]() と
と![]() の公約数を
の公約数を![]() とする。すると、
とする。すると、![]() はどちらも
はどちらも![]() の倍数となる。ここまでは大丈夫か?」
の倍数となる。ここまでは大丈夫か?」
A「うん、ここは高校でもやったから」
D「俺もいいぞ」
X「じゃあ、ディーに質問だ。![]() が
が![]() の倍数であることを数式で表してみてくれ」
の倍数であることを数式で表してみてくれ」
D「そうだな…」
D「…こうか?」
A「![]() って何?」
って何?」
D「![]() は…何かしらの自然数だな。
は…何かしらの自然数だな。
そうか、それも書かないといけねぇわけだな」
を自然数として
X「そのとおりだ。今は![]() が自然数となっているから
が自然数となっているから![]() も自然数になる。同様に
も自然数になる。同様に![]() はこのように表される」
はこのように表される」
を自然数として
X「あとは2つの差を取る」
X「よって、![]() が成り立つ。さて、
が成り立つ。さて、![]() はすべて自然数であったことと、
はすべて自然数であったことと、![]() は
は![]() より大きいことから
より大きいことから![]() も自然数になることが分かる」
も自然数になることが分かる」
A「そうすると、![]() と
と![]() を掛けたら
を掛けたら![]() になるから…」
になるから…」
D「それって、![]() しかないじゃねーか!」
しかないじゃねーか!」
X「そう。だから![]() が成り立つ。さて、
が成り立つ。さて、![]() は
は![]() と
と![]() の公約数だったから、これが
の公約数だったから、これが![]() ということは
ということは![]() と
と![]() が互いに素であるということが証明された」
が互いに素であるということが証明された」
M「このように、互いに素であることを確かめるときには![]() の倍数としてから
の倍数としてから![]() であることを示すことが常套手段ね」
であることを示すことが常套手段ね」
X「![]() と
と![]() が互いに素であることも確かめよう。そうすれば十分だな」
が互いに素であることも確かめよう。そうすれば十分だな」
A「どうして?」
M「もし、![]() と
と![]() が互いに素であるとすると、
が互いに素であるとすると、![]() と
と![]() も互いに素。
も互いに素。
そうすると![]() なのだから、
なのだから、![]() と
と![]() が互いに素でなければ、その公約数を
が互いに素でなければ、その公約数を![]() とすると
とすると![]() より
より![]() も
も![]() の倍数となるわね。これは
の倍数となるわね。これは![]() と
と![]() が互いに素であることに矛盾するわ」
が互いに素であることに矛盾するわ」
D「…つまり?」
M「![]() の倍数同士の差は
の倍数同士の差は![]() の倍数になる。
の倍数になる。
だから、![]() のどこかに互いに素でないものがあれば、最後の一つも足したり引いたりするから同じ公約数を持つのよ」
のどこかに互いに素でないものがあれば、最後の一つも足したり引いたりするから同じ公約数を持つのよ」
D「偶数同士の足し算は偶数になる。3の倍数同士の足し算は3の倍数になる。それと同じか…。
今は![]() と
と![]() が互いに素だと分かった。あとは
が互いに素だと分かった。あとは![]() と
と![]() で示せれば、最後の一つも自然と互いに素だって分かるってことか」
で示せれば、最後の一つも自然と互いに素だって分かるってことか」
X「納得できたようだな。それでは示していこう。」
であることから
となる。と
は互いに素なので、あとは
と
が互いに素であることを示せばいい。これは
(
は自然数)とおくと
となることからとなることから示される。
が
と互いに素であるので、その積である
も
と互いに素となる。
X「まぁ、このような形か…。」
A「うーん、なんとなく分かる気がするんだけど…」
D「一つ一つ見ていくとするか」
そう言って、アキとディーは数正の証明を確認することにしました。
M「…成長したわね、二人共。
前だったら分からないって言って止まっていたのに、今では少しずつ自分から確認しようとしている」
X「そうだな。
ところで、真理の考えた問題、というのは何だ?」
M「そうね、その話をしましょう。
今示したことは原始ピタゴラス数が無数に存在することの証明だったけど、最も大事だったところは『2つの数の差が![]() となる』こと。
となる』こと。
言い換えると、これは『3つの自然数のうち2つの差が![]() となる原始ピタゴラス数』の存在証明ね」
となる原始ピタゴラス数』の存在証明ね」
X「確かにそうだな」
M「私が考えた問題は2つ。
その一つが、『3つの自然数のうち2つの差を![]() にしたらどうなるか』なのよ」
にしたらどうなるか』なのよ」
ということで、原始ピタゴラス数で2つの自然数の差が1となるものの存在証明でした。
続きはこちら!
日曜数学 Advent Calendar 2020→明日はコロちゃんぬさんです!(*´∀`*)
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件