こんばんは、satoです。
本日の夕方から数学の賞・アーベル賞のセレモニーが行なわれます。
今年受賞したのはフェルマーの最終定理を解決したことで有名な「楕円曲線」の研究者・アンドリュー・ワイルズです。
それにちなんで、前回に引き続き本日も「楕円曲線」の面白さについて書いてみます。
今回は最初に数式なしで色々話をして、最後の方に数式を使って話を進めていきます。数学が好きな人は最後まで見てくださればと思います。
楕円曲線とは?
まず、前回話した楕円曲線と楕円の関係について大雑把に書きます。
「楕円曲線」は楕円とは異なるのですが、これについてもう少し事情を書いてみましょう。
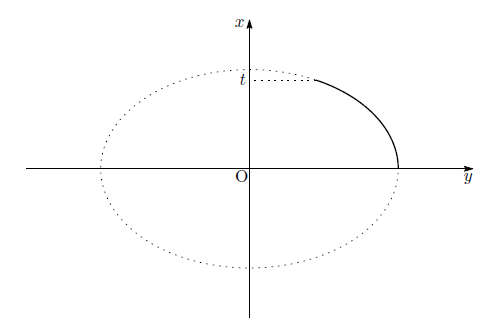
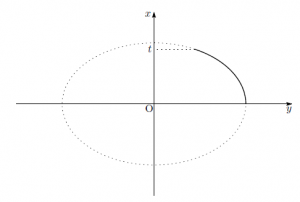
楕円とは上のような「少し潰れた円」なのですが、この楕円の弧の長さを計算する際に、楕円積分というものを考える必要があります。この楕円積分というのは「![]() 座標から弧の長さを計算する」関数です。これは高校で学ぶような積分計算が簡単に出来ず、この計算のために一つの研究が進んだほどです。
座標から弧の長さを計算する」関数です。これは高校で学ぶような積分計算が簡単に出来ず、この計算のために一つの研究が進んだほどです。
で、この楕円積分の逆関数、つまり「楕円の弧の長さから![]() 座標を出す」関数が楕円関数です。これには色々なバリエーションがあるのですが、一番有名、かつ分かりやすいのがワイエルシュトラスの楕円関数(ワイエルシュトラスの
座標を出す」関数が楕円関数です。これには色々なバリエーションがあるのですが、一番有名、かつ分かりやすいのがワイエルシュトラスの楕円関数(ワイエルシュトラスの![]() 関数)です。
関数)です。
余談ですが、アーベル賞の由来となっているニールズ・アーベルは「五次方程式が代数的に解けない」ことを最初に示した人という話は聞いたことがあるかもしれません。実は、この楕円関数を最初に発見した人でもあり、楕円積分の一般化である「アーベル積分」とその逆関数である「アーベル関数」を研究したことでも有名です。
この楕円関数とその微分はある方程式を満たします。
その方程式から作られる図形こそが楕円曲線です。どんな数式かというと…
![]()
です。(厳密には定義する体によっては別の形にしなければならないのですが)
というわけで、楕円曲線は「楕円の弧の長さ」と関連する曲線でした。あとで、円の場合でこの話をもう少し解説したいと思います。
楕円曲線の面白さ
さて、楕円曲線には様々な特徴があります。
まず、楕円曲線の(無限遠点を含めた)各点には「演算」が存在します。演算が存在する、というのは…たとえば私達がよく知っている平面や3次元空間には「平行移動」や「回転」という操作があります。このような操作が楕円曲線の上にもある、ということです。余談ですが、このような演算が存在する(専門用語で「群構造を持つ」と言います)ような「代数方程式の解」からなる図形(代数多様体)のことをアーベル多様体といいます。またしてもアーベルが出てきましたね…。
そして、楕円曲線には数学のいろいろな分野と関連しています。
たとえば、前回も書いたように楕円曲線がモジュラー関数と関連しているという「谷山-志村予想(モジュラリティ定理)」によってワイルズはフェルマーの最終定理を解決するに至りました。また、この記事にも書きましたが、ガウスは楕円曲線の周期と算術幾何平均の逆数が超幾何関数の特殊値を介して一致することを示しています。
このように楕円曲線では様々な性質が成り立つのですが、これを基に各分野で多くの研究がされています。いわば、楕円曲線が「発見の源」となっているんですね。
ミレニアム問題の一つであるバーチ・スウィナートン=ダイアー予想(BSD予想)は楕円曲線に関する重要な予想です。
モジュラリティ定理やBSD予想を説明するには「ゼータ関数」について話をしなければならないので、ここでは省略します。
数学的にも面白い楕円曲線ですが、実は楕円曲線暗号などといった暗号理論を介してコンピュータのセキュリティにも強く関わっています。そう、この社会にも楕円曲線が関わっているのです。
現在の主流な暗号理論(RSA暗号)は「素因数分解の難しさ」によって保証されているのですが、これは量子コンピュータといった「並列演算が可能となるコンピュータ」が出てくると解かれてしまう危険性があります。
しかし、楕円曲線暗号の安全性は「離散対数問題」の難しさによって保証されていて、これを解く(実用的な)アルゴリズムがまだ見つかっていないため、RSA暗号より安全なものとなっています。
しかも、処理速度も速いようです。
長くなりましたが、まとめると
楕円曲線は数学的にも重要な位置を占めていて、現在も各分野から研究されている。
さらに、セキュリティの強固な暗号理論の核としても使われ、社会にも強く関わっている。
というように、楕円曲線というのは数学内外にとても大きな影響を及ぼしているのでした。つまり、前回の楕円と合わせると
「楕円形」は我々の生活に大きく関わっている
というわけです。
(数学好きな人向け)楕円積分→楕円関数→楕円曲線の流れのもう少し詳しい解説
さて、最後に数学好きな人向けにもう少し数式を用いて説明をしたいと思います。
まず楕円の方程式は
![]()
となります。この方程式の弧の長さは
![Rendered by QuickLaTeX.com \[\int_0^t\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx=\int_0^t\sqrt{1+\left(\frac{(b^2/a^2)x}{y}\right)^2}dx\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-ac579f3cecfdf9c8f39e386134386a4d_l3.png)
![Rendered by QuickLaTeX.com \[=\int_0^t\sqrt{1+\frac{(b^2/a^2)^2x^2}{y^2}}dx\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-49adae4a3db8b7987f165760ce49daa8_l3.png)
![Rendered by QuickLaTeX.com \[=&\int_0^t\sqrt{\frac{y^2+(b^4/a^4)x^2}{y^2}}dx\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-8a4d498383664f08cc6f9ec6f3a88166_l3.png)
![Rendered by QuickLaTeX.com \[=\int_0^t\sqrt{\frac{y^2/b^2+(b^2/a^2)x^2/a^2}{y^2/b^2}}dx\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-6e312ae485f2671635acd4f5c9d1d0a0_l3.png)
![Rendered by QuickLaTeX.com \[=&\int_0^t\sqrt{\frac{1+(1-(b^2/a^2))x^2/a^2}{1-x^2/a^2}}dx\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-87cec7fd99afc8a4f0cbd1e9bad131c0_l3.png)
となります。離心率(焦点が原点からズレている割合)を![]() として、変数変換をすると
として、変数変換をすると
![]()
となります。これが下図のような楕円の弧の長さになります。
これは第二種楕円積分と呼ばれるもので、初等的な関数では計算できません。これはつまり四則演算や初等関数のような値が分かっている関数では求められないという意味です。
でも、楕円は色々なところで出てくるのでその弧の長さが計算できるようにしたい…ということで楕円積分が計算されました。
ところで、離心率が![]() となる場合、つまり「円」ではどうなるか、と言いますと。
となる場合、つまり「円」ではどうなるか、と言いますと。
![]() とすると上の積分は
とすると上の積分は
![]()
となります。この積分の中身、被積分関数をどこかで見た、という人は大学の勉強をしている人ですね。
この関数は三角関数の逆関数![]() の微分なのです。言い換えると、上の積分は
の微分なのです。言い換えると、上の積分は![]() です。
です。
つまり、円の弧の長さを求める時には逆三角関数を用いればいいのです。この逆関数は三角関数![]() です。このことから楕円関数というのは三角関数
です。このことから楕円関数というのは三角関数![]() の親戚になります。
の親戚になります。
さて、![]() の微分は
の微分は![]() ですが、この二つの関数は
ですが、この二つの関数は
![]()
を満たします。つまり、![]() とその微分
とその微分![]() は円周
は円周![]() にあるわけです。これが「円曲線」というものです。
にあるわけです。これが「円曲線」というものです。
というわけで、円の場合は、
弧の長さを求める関数![]() →その逆関数
→その逆関数![]() →関数とその微分が満たす方程式
→関数とその微分が満たす方程式![]()
という風に対応していて、最後の方程式は円の方程式になっているわけです。これと同じように楕円の場合は
楕円の弧の長さを求める関数(楕円積分)→その逆関数(楕円関数)→関数とその微分が満たす方程式![]() (楕円曲線)
(楕円曲線)
というように対応しています。しかし、満たす方程式は幸か不幸か楕円の方程式とは異なるんですね。
こうやって見ると…楕円って、深く見ると本当に神秘的ですよねヾ(*´∀`*)ノ
参考文献(Webサイト)
それぞれのサイトでもっと詳細な情報が書かれています。あと、『数学ガール-フェルマーの最終定理』にも楕円曲線の定義が書かれています。こちらでは有限体を用いて、谷山-志村予想の導入を説明しています。とても読みやすい本ですので、ぜひご一読あれ(/・ω・)/
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 聖書&御言葉2024年4月26日真の「信仰」とは?科学者もスッキリ『聖書の信仰観』
聖書&御言葉2024年4月26日真の「信仰」とは?科学者もスッキリ『聖書の信仰観』 数学2024年4月25日御心を探して。私は何をしたいのか?~研究者の進路に悩む人へ~
数学2024年4月25日御心を探して。私は何をしたいのか?~研究者の進路に悩む人へ~ スポーツ2024年4月24日個人か、全体か。試合を通して感じた犠牲と愛
スポーツ2024年4月24日個人か、全体か。試合を通して感じた犠牲と愛 日常生活2024年4月23日飛行機に乗っていて悟ったこと。~飛行機はどうして飛ぶのか~
日常生活2024年4月23日飛行機に乗っていて悟ったこと。~飛行機はどうして飛ぶのか~