摂理人satoも注目・「楕円曲線」とは？？初級編 | 摂理研究所/キリスト教福音宣教会

こんばんは、satoです。

数学界には「ノーベル賞」がないことを知っている人は割と多いと思います。
その理由は定かではありませんが…(´・ω・｀)数学界で一番有名なのが「フィールズ賞」です。ただ、この賞は…

・4年に一度与えられる

・「若手の研究者の優れた功績に対する賞賛と奨励」という目的のため「40歳未満」という制限がある

・共同で業績を挙げても一人しか受賞されない(例:マイケル・アティヤーとイサドール・シンガーは「指数定理」という革新的な定理を証明したが、フィールズ賞を受賞したのはアティヤーのみ)

・賞金額が違う(ノーベル賞が1億円、フィールズ賞は200万)

など、ノーベル賞とはだいぶ性格が異なる賞です。

そんな中、2003年に新たな数学の賞が作られました。それがアーベル賞です。
この賞は「数学全般に関わる業績」に対する賞で、年に一度選定されます。年齢制限もなく、賞金もノーベル賞と同じ1億円という非常に高額なものです。
さらに、共同の業績を挙げた人は全員選ばれます(先のアティヤーとシンガーは指数定理の業績でアーベル賞を2004年に受賞)
このように、アーベル賞はノーベル賞と性格がかなり近く、「数学界におけるノーベル賞」と言っても問題ないものとなっています。(名前も似てますよね…(笑))
さらに、ノーベル賞はスウェーデンとノルウェーの組織が選定しますが、アーベル賞もノルウェーで選定されます。

というわけで、歴史は浅いものの数学界におけるとても栄誉ある賞の一つが「アーベル賞」です。
これまでも著名な数学者が受賞されていました。フィールズ賞受賞者もかなり多いです。

今年も3月15日に受賞者が発表されました。今年受賞したのはアンドリュー・ワイルズです。
この名前、どこかで聞いたことのある人もいるのではないでしょうか？そう、フェルマーの最終定理を証明したことで有名なアンドリュー・ワイルズです。フェルマーの最終定理とは

$3$ 以上の自然数 $n$ に対して

$x^n+y^n=z^n$

を満たす自然数 $x,y,z$ は存在しない。

という問題です。これが証明されるまでに約４００年かかった、というくらい難問です。

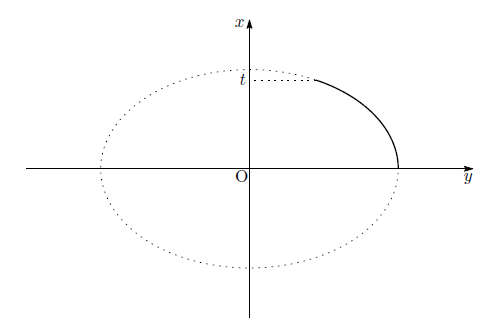
ワイルズは「楕円曲線」というとても面白い曲線の研究者です。
フェルマーの最終定理の証明にも「楕円曲線にはとても良い性質がある」という「谷山-志村予想(現在はモジュラリティ定理と呼ばれる)」が必要とされ、これをワイルズが証明したことでフェルマーの最終定理が解決したのでした。
今回ワイルズがアーベル賞を取った業績も、フェルマーの最終定理を楕円曲線のモジュラリティ定理を証明することで解決する、という数論における新たな手法の開拓というものなのです。

せっかくなので、今回のアーベル賞受賞に際して楕円曲線がどんな風に面白いのかについて少し説明してみます。
と言っても、とても高度な数学の話になるので最初は楕円について話してみます。

目次非表示

楕円とは

楕円とは

このように、少し潰れた円のことを言います。
楕円というのは様々なところに存在しています。地球も遠心力で円形でなく楕円形になっています。
卵とか亀の甲羅も楕円形に近いです。
あと、人間は色々なところが「楕円形」になっています。絵を描いている人はわかると思いますが、人間のそれぞれのパーツを直線で書くより「楕円」にするとより近くなりますよね？

このように、楕円形は結構身近にあるものです。

楕円の性質として、円の中心のような「焦点」が二つあります。片方の焦点から光を出すと、もう一つの焦点に集まります。
だから焦点に紙を置くと光の熱で「焦げる」わけです。焦げる点だから焦点。

こういう「何かを一点に集める」という性質は様々に活用されます。
パラボナアンテナは電波を焦点に集めることで受信し、テレビを見れるようにします。逆に焦点から電波を出すと、平行に進みます。
パラボナアンテナの面は放物面ですが、この放物面も実は「楕円形」の仲間なんです。
楕円形、放物面、それと双曲面(反比例のグラフみたいなものです)は専門用語で二次曲面という一つの図形になります。
こう見ると、楕円というのは生活にもとても関わっているんですね。

ちなみに、ちょっと専門的な話をすると…。
楕円と放物線、双曲線は無限遠点まで考慮するとすべて「楕円」になります。
放物線は楕円の端っこが無限遠点、双曲線は無限遠点が楕円の中にある、という状態です。

さて、最初に話した「楕円曲線」は楕円とは違うんです。
もちろん、関係はあるんですけどね…ここから先が深い話になるのです。

ちょうど明日からアーベル賞のセレモニーが始まるようなので、明日はその話をしたいと思います。