数学のA・B・C その１ | 摂理研究所/キリスト教福音宣教会

こんばんは、satoです。
今日は数学のA・B・Cというタイトルで
「数学(特に大学でやるような難しい数学)は何をやっているのか？」ということを書いてみようと思います。
今回書きたいのは数学というのはたくさんあるパターンを一つの数式で表す、そして「その背景にある法則」を考えるということをしているって話です。

目次非表示

「ABC予想」
まずは、$c$と「$a,b,c$の積」を比べてみる
ちょっと難しいことをします。

「ABC予想」

皆さんはABC予想という数学の問題をご存知ですか？
この予想は京都大学数理解析研究所の望月新一教授がその証明論文をインターネット上に公開した、ということで2012年に話題になりました。
望月教授が論文を発表した際に数学界では相当反響を呼んだのですが、それは「ディオファントス解析の中で一番重要な問題」とされているからです。
では、ABC予想とはどんな問題なのでしょうか？
ABC予想とは次の数式の性質についての問題です。

$a+b=c$

数式に「 $a,b,c$ 」とつくからABC予想、シンプルでしょ？(笑)
ちなみに、 $a,b,c$ には $1,2,3,4,ldots$ という数が入ります。数学用語だと「自然数」といいます。あと、 $a$ と $b$ は互いに素(公約数が $1$ )という条件があります。
「 $2$ つの互いに素な自然数を足す」という簡単な数式ですが、実はこの中にとてもおもしろい法則があるのです。

先にその法則を書くと、次のようになります。
εを任意の正の数とします。このとき、次の不等式を満たす $(a,b,c)$ は有限個しかありません。

$c>text{rad}(abc)^{1+epsilon}$

…たぶん、数学が苦手な方にとっては非常に目を逸らしたくなるような数式ですね(^_^;)
これから、少しずつ説明していきます。

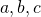まずは、 $c$ と「 $a,b,c$ の積」を比べてみる

たとえば、 $a$ を $2$ 、 $b$ を $3$ とします。そうすると、 $c$ は $2+3=5$ になります。
この $5$ と「 $a,b,c$ の $3$ つの積」…ここでは $2times3times5=30$ を比べると

$5<30$

となります。実はこれ、 $a,b$ が( $a=b=1$ 以外では)どのような数でも成り立つのです！

「いや、当たり前じゃん！」

そうなんです、これは中学くらいで習うことですぐに示せます。
(詳しい証明は追記で書きます)

ちょっと難しいことをします。

では、少し難しいことを考えましょう。
今、 $a,b,c$ の積と $c$ を比べましたが、これを「 $a,b,c$ の各素因数の積」と比べるとどうなるのでしょうか？
素因数というのは、自然数を素因数分解したときに出て来る素数( $1$ とそれ以外でしか割れない自然数)のことです。いくつかの数で考えてみましょう。

$45=3times3times5$ なので、素因数は $3$ と $5$ 。

$12=$ 2times2times3 $なので、素因数は$ 2 $と$ 3 $。$ 2015=5times13times31 $なので、素因数は$ 5 $と$ 13 $と$ 31 $。このように、全ての自然数は素因数の積に分解することができます。それも、ただひとつのパターンで。これを<strong>素因数分解の一意性</strong>と言います。さて、比べてみましょう。さっきの例だと、$ a=2,b=3,c=5 $はどれも素数なので、「$ a,b,c $の各素因数の積」はさっきと同じ$ 30 $です。なので、結果は同じ。では、他の数ではどうでしょうか？皆さんも小さな数で試してみましょう！$ a=3,b=4 $だと、$ c=3+4=7 $、「$ a,b,c $の各素因数の積」は$ 3×2×7=427<42 $、やはり積の方が大きい。$ a=1,b=8 $だと、$ c=9 $、「$ a,b,c $の各素因数の積」は$ 1×2×3=69>6 $、これも…あれ？これは、積の方が小さいですね！そう、実は$ c $と「$ a,b,c$の各素因数の積」は大小が逆転することがあるのです！