「一次元上げる」と、こんなにもすごい！ | 摂理研究所/キリスト教福音宣教会

一次元上げたら、次元の低いものはすべて入る。

おはようございます、satoです。

今日は鄭明析先生のこの明け方の箴言について話をしたいと思います。

＜一次元の差＞はとてつもない。

＜最高に大きいもの＞を得たら、「次元の高いもの」だけではなく「その下の次元のもの」まですべて得たことになる。

目次非表示

ホイットニーの定理
考えの次元を上げると…

ホイットニーの定理

数学には多様体という図形があります。この図形は簡単に言うと地球のように、地図を貼り合わせてできるような図形ということです。これについて自分なりに説明をしたいと思います。

まず $RB^{2n}$ というのはユークリッド空間という図形で、すべての基本となる空間です。たとえば、 $RB^3$ というのは $(0,1,2)$ や $(1,2,3)$ のように、点の位置が3つの実数の組みで表せる図形です。つまり、私達が生きている3次元空間のことです。
これと同じように、 $RB^{2n}$ というのは $2n$ 個の実数の組で点の位置を表せます。

先に多様体を「地図を貼り合わせてできる図形」と話しましたが、 $n$ 次元多様体というのは、図形の一部が $RB^n$ の一部と同じように扱える…つまりその部分の点の位置を $n$ 個の実数の組で表せるということを意味します。この「 $n$ 個の実数の組」の付け方を局所座標と言いますが、この局所座標系が「地図の組」です。

先程地球の地図の話をしました。
地球全体を一つの地図で表そうとすると、大きさが歪んたり、元々一点だった北極点が直線になったり、色々不都合が起こります。すべての図形の位置を正確に表そうとしたら、2つの地図が必要になります。
ところで、地図は「緯度」と「経度」という2つの数字で位置を表すことができる、つまり $RB^2$ の一部と同じなのです。
だから、地球(3次元球面)は2次元多様体ということができます。

ちなみに、「 $n$ 個の実数の組」の付け方には一つ大事なことがありまして。
図形の2つの部分があって、それぞれに「 $n$ 個の実数の組」の付け方があるとします。ところで、この2つの部分には共通部分(重なっている部分)があるとします。このとき、2つの「 $n$ 個の実数の組」の付け方には対応があるということが大事なのです。これがないと、片方の地図を見て、もう一つの地図の位置が分からない、ということがありますからね…。
実際、地図は重なっている部分を合わせるとちゃんと(縮図を除いて)合わさりますよね。

この図形に対して次のような定理が成り立ちます。

任意の $n$ 次元多様体は $RB^{2n}$ に埋め込むことができる。

これをホイットニーの(埋め込み)定理と言います。ちなみに、埋め込むとはここでは「その空間で実際に作れる」と思ってください。たとえば、 $n=2$ のときを考えると、3次元球面はボールの表面とか地球とか、今自分たちが生きている「3次元空間 $RB^3$ 」にありますよね。つまり、3次元空間に埋め込まれています。

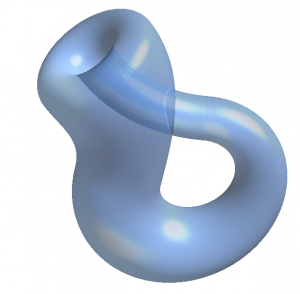
3次元空間に埋め込めない2次元多様体の例はクラインの壺です。

クラインの壺です。交差しているように見えますが、実際には交差していないです。ちなみに、これは「クラインの壺」というフリーソフトを使って作った図です。

こんな感じの図形です。ただし、自己交差しているように見えますが、実際のクラインの壺は自己交差をしていません。
なので、この図形の面をたどると、外側から内側へ、そしてまた外側へ行くという不思議な現象が起こります。ちょうどメビウスの輪が表裏のない図形であるように、クラインの壺は外側・内側がない図形なのです。

で、この図形は3次元空間で再現しようとするとどうしても自己交差してしまいます。だから、これは4次元以上の空間でしか再現できないんです。

ここまで長くなりましたが…数学的にも次元を上げると、次元の低い図形はすべて入るようになっているのです。

考えの次元を上げると…

これと同じように、考えの次元を上げると、小さな問題はすべて解決しています。
御言葉を聞いていると自分の問題が解決している、ということがありますが、これは御言葉が神様の次元の視点から見たものなので、それより次元が低い自分の問題の答えが含まれているからなのです。
あ、次元という言葉が分かりにくい時は「スケール」と読み替えると良いです。自分のスケールで考えるか、家族のスケールで考えるか、民族か、世界か…それとも、それ以上か。

自分が神様の考えに触れるといつしかスケールが高くなります。
実際、今日ある御言葉を聞いていたのですが、何回も聞いたはずの御言葉が深く理解されました。思わず「あーーーーーー！」と言いそうになりました（笑）
それは、私が神様の御言葉を聞いて、いつの間にか考えのスケールが高くなっていたからなのでしょう。

自分がどの次元の考えで生きるか。
それによって、御言葉は様々な姿を見せます。しかし、一番面白いのは神様の視点から見たときです。

その次元を目指して、今日も頑張りたいと思います。メビウスの輪のように、神様には裏表なく接したいですね（笑）