おはようございます、satoです。
間が空きましたが前回に引き続き柏原正樹教授の研究について少しでも分かるように説明を試みたいと思います。
復習
ICM2018にて「生涯に渡って突出した数学的功績を出した」人に贈られるチャーン賞を京大の柏原正樹教授が受賞しました。
これは日本人としては初めてであります。
前回書きそびれていましたが、柏原正樹教授は「京都賞」も受賞していまして、それに続く栄誉です。
柏原正樹教授が研究されたのは「代数解析学の理論の構築と表現論への応用」です。
代数解析学の要となる微分作用素(関数や関数からなるベクトルに対して微分する、という作用をするもの)について前回は説明しました。
今回は、代数解析学の研究対象となる微分方程式について説明を試みたいと思います。
微分と積分の関係
まずは、微分と対になる「積分」について説明していきます。
接線から元の関数を復元する
たとえば、二次関数![]() があったとします。この関数のグラフは次のように「放物線」になる、というのを高校で勉強しました。
があったとします。この関数のグラフは次のように「放物線」になる、というのを高校で勉強しました。

ところで、この関数を微分すると![]() となります。
となります。
この微分したあとの関数を「導関数」というのですが、これは各点のグラフの接線の傾きを出す関数になっています。
たとえば、![]() のとき
のとき![]() の接線の傾きは2になります。
の接線の傾きは2になります。
![]() における接線、ということは接線は
における接線、ということは接線は![]() で接している、ということが分かるので、
で接している、ということが分かるので、![]() における接線の方程式は
における接線の方程式は
![]()
となります。これを整理すると
![]()
となるわけです。
たとえば、![]() のときの接線の方程式は
のときの接線の方程式は![]() ですし、
ですし、![]() のときの接線は
のときの接線は![]() 、つまり
、つまり![]() 軸になります。(これは上のグラフからも分かりますね)
軸になります。(これは上のグラフからも分かりますね)
次の図は、![]() のときを繋げたものです。
のときを繋げたものです。
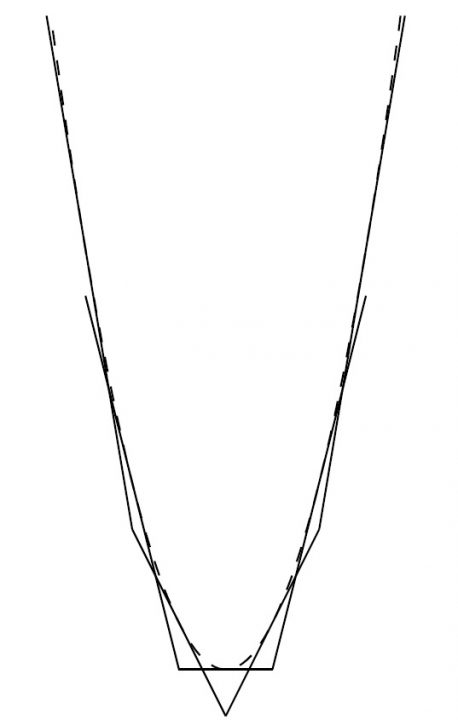
ところで、これらの接線を結んだものをよく見ると元の放物線と類似していますね。特に両端辺りは…。
さらに細かく接線を取ると放物線に近くなる…そんな感じもします。
積分の考え方
実は、この考えこそが積分の定義なのです。
より詳しくはこのようになります。
![]() のとき、
のとき、![]() でした。
でした。
ここで、「ごく小さい区間での接線」を![]() とします。(
とします。(![]() の部分が
の部分が![]() となっていて、この極小の差を固定する感じです)
となっていて、この極小の差を固定する感じです)
そして、この![]() を「端から端まで繋げていく」ことを
を「端から端まで繋げていく」ことを
![]()
と書きます。感覚としては「ある点の十分近くでの接線を繋げていくと元のグラフが再現できる」ので、これが元の関数になることが期待されます。
ただし、ここで分かるのは正確には「グラフの形」だけです。
たとえば、![]() も微分すると
も微分すると![]() となります。よって、
となります。よって、![]() は
は![]() である可能性もあるのです。
である可能性もあるのです。
これが積分定数の不定性です。以上から
![]()
が成り立つ…というわけです。
このように、![]() に対して、「接線を繋げていくと元の関数のグラフが再現できる」ということが
に対して、「接線を繋げていくと元の関数のグラフが再現できる」ということが
![]()
に現れている、というわけです。
ここで大事なのは導関数という「局所的な情報」によって元の関数のグラフの形が作られるという考え方です。
もう少し細かく
ところで、導関数をもう一回微分すると二階導関数が得られます。(※二回、ではありません笑)
二階導関数は「導関数の変化」の情報を持っているのですが、これは「導関数=接線の傾き」ということから「接線の傾きの変化」が分かります。
たとえば、![]() のとき導関数は
のとき導関数は![]() ですが、これをもう一回微分すると
ですが、これをもう一回微分すると![]() となります。
となります。
このことから、特に「接線の傾きが常に増加し、その増加率は一定である」ということが分かります。
このように2次関数![]() の2階導関数は
の2階導関数は![]() と定数になることから、「放物線は接線の増加率が一定となる形である」という特徴づけができます。
と定数になることから、「放物線は接線の増加率が一定となる形である」という特徴づけができます。
このように、関数の微分、そのまた微分、…という情報から元の関数の情報を復元することができる、ということがあります。あります。
(これは「テイラー展開」と呼ばれる話に繋がります)
微分方程式
さて、たとえば指数関数![]() は「微分すると元の関数と等しくなる」という特徴があります。つまり、
は「微分すると元の関数と等しくなる」という特徴があります。つまり、
![]()
が成り立ちます。このように「導関数、二階導関数、…![]() 階導関数が満たす関係式」のことを微分方程式といいます。
階導関数が満たす関係式」のことを微分方程式といいます。
ちなみに、![]() を「関数
を「関数![]() を掛ける」という作用素として考えると、上の式は
を掛ける」という作用素として考えると、上の式は
![]()
となります。これは(定数係数)線形微分方程式と呼ばれる形になります。
微分方程式はいわば「ある関数の局所的な情報」であり、それを解くということは「局所的な情報から元の関数を復元する」ことに繋がります。
これは先程「導関数がグラフの形を作る」と書いたことと似ています。
ちなみに、物理学の中でも微分方程式は多く出ています。それは、ある関数が「時間ごとの位置の情報」を表すものだとすると、その導関数は「時間ごとの速度」、二階導関数は「時間ごとの加速度」を表すからです。
放物線の二階導関数の話を物理学に適用すると、等加速度運動したときの距離の変化になります。
特に「物体を投げたときの軌道」は等加速度運動(掛かるのは重力のみ)で、その軌道は放物線となります。
※実際に放物線になるのは物体の「水平方向」の移動は(この方向には力が働いていないので)等速運動、「垂直方向」の移動は重力のみが影響を与え、重力は重さによって一定に定まることから来ています。
現在の未解決問題の中にも微分方程式が関わるものがあります。
さて、代数解析学が扱うD加群の範囲は(多項式関数、もしくは解析関数係数)線形微分方程式です。
(さらに拡張して「代数的非線形微分方程式」にまで拡張しよう、という構想を佐藤幹夫先生は持っていたようです)
これについて、どのような研究をしていったのか、これについて次回は書いていこうと思います。
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件