四角形は「角の付いた」円だという話。

SHARE

おはようございます、satoです。

今日は鄭明析先生の明け方の箴言

＜円形と楕円形＞を基本としてさまざまな形と形象が成される。
楕円形を縦にした形と横にした形だ。また＜四角形＞は一種の「角（かく）のある円形と楕円形」だ。

について、思い出した話を書きたいと思います。
題して「円の極限は正方形になる」ということです。

理系の人は習ったことがあると思いますが、円の方程式はx^2+y^2=1です。この式の意味は「原点からの距離が1である」ということです。これは円の定義でもあります。

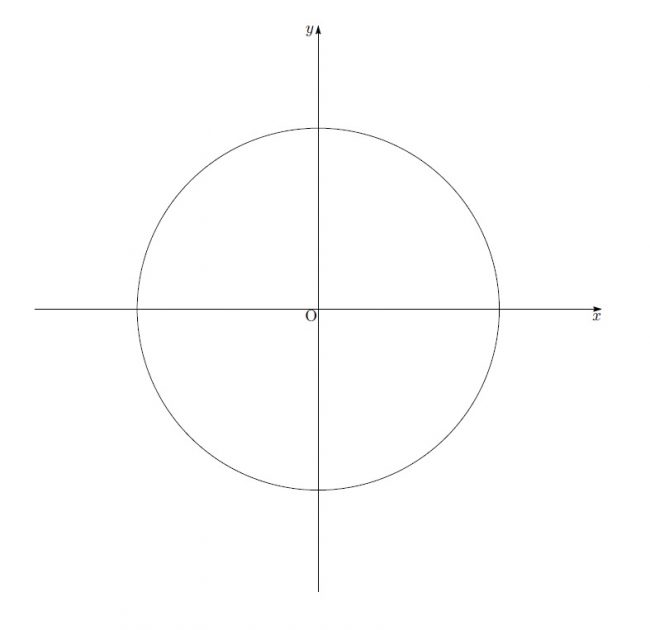
図を描くと、このような形になります。ところで、今「xとyを2乗して足して」していましたが、これをもっと大きくするとどうなるでしょうか？
つまり、「xとyをそれぞれn乗してから足す」のです。

実際にやってみましょう。

x^4+y^4=1というように、2乗を4乗にしてみると…

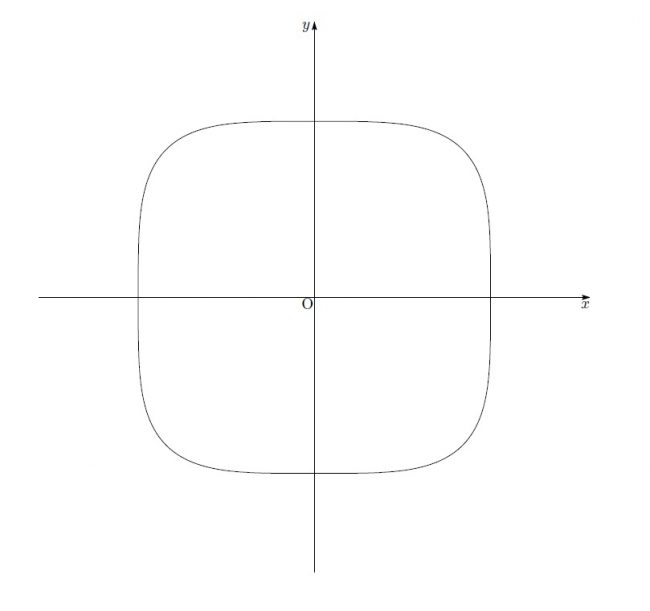
こんな図形になります。なんだかグミみたいですね笑
もう少し増やしてx^6+y^6=1とすると、

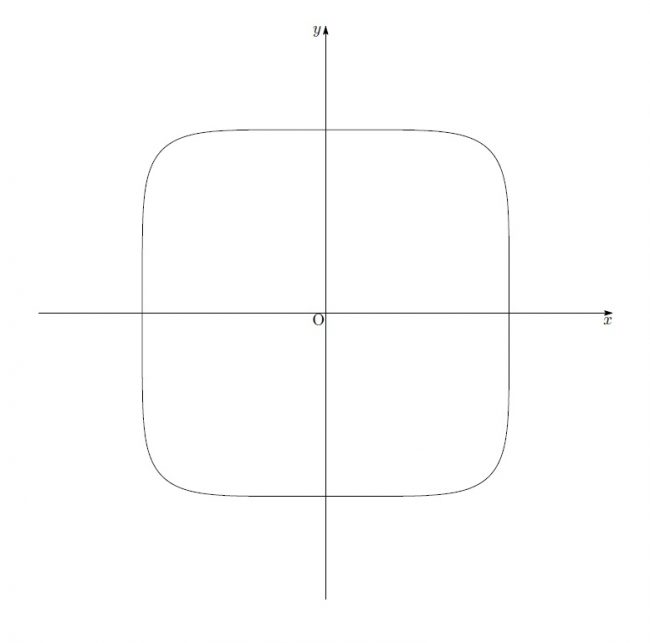
こうなります。

ここでお気づきの方もいるかもしれませんが、この図形、段々と正方形に近づいています。
実際、x^8+y^8=1にしてみると

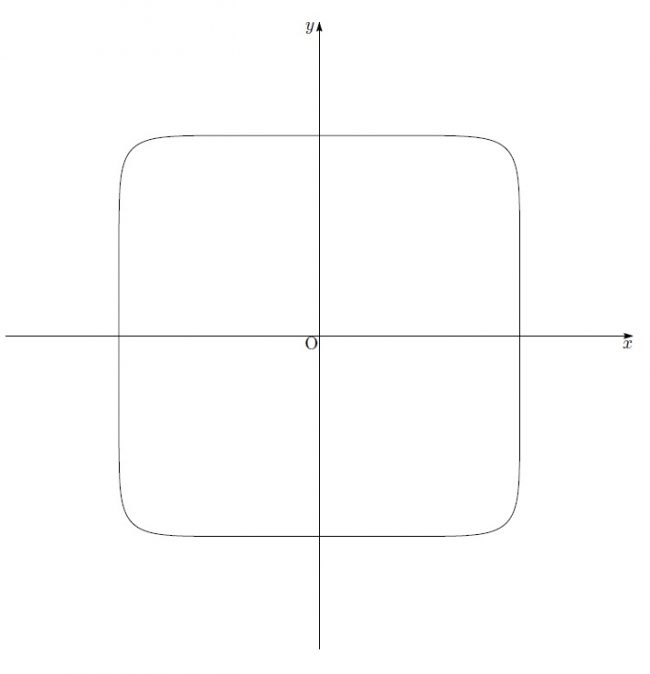
さらに正方形っぽくなっています。もっと大きくx^{50}+y^{50}=1とすると

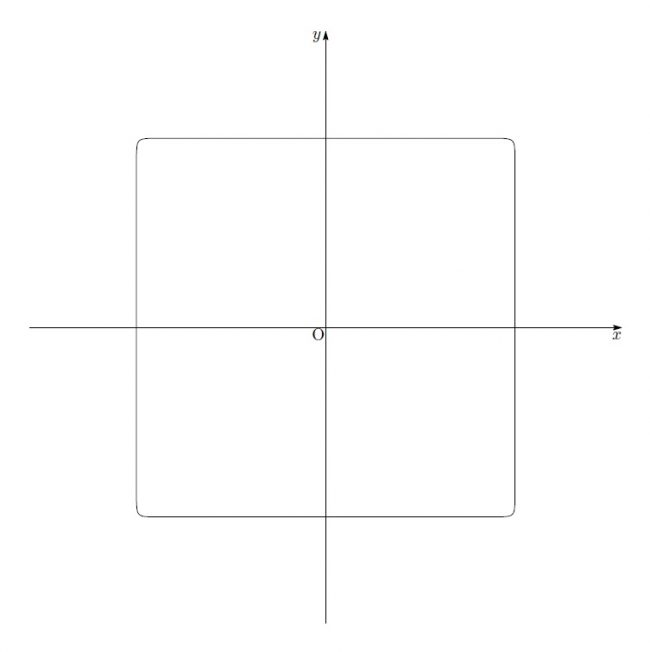
もはや、正方形とほとんど変わりありません。もっともっと大きくするともっともっと正方形に近づいていきます。
(残念ながら、作図ソフトの関係でここまでが限界でした^^;)

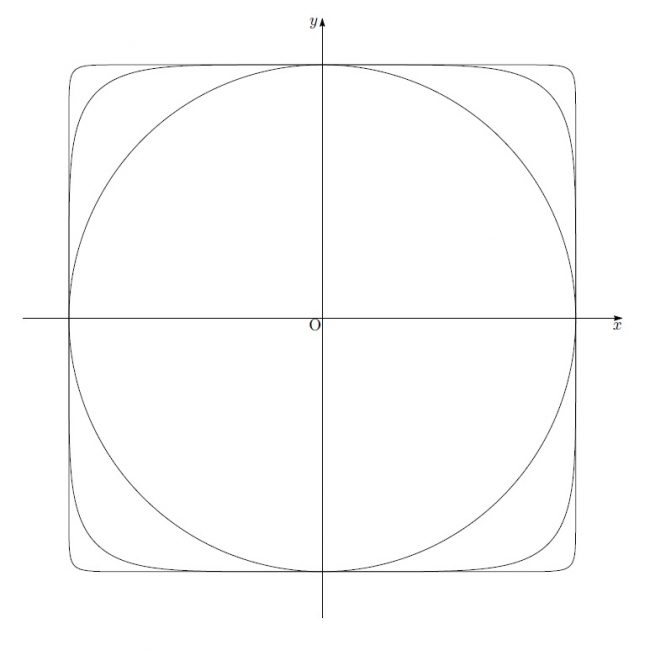
x^2+y^2=1、つまり円から始まって、べきのところを大きくすると、段々と正方形になっていくことが分かります。
この図は6乗と30乗のときの図を載せました。

ちゃんと数式にすると、

    \[x^{2n}+y^{2n}=1\]

のnを限りなく大きくすると、正方形になるのです！
ところで、正方形の式はどのようになるか、と言いますと…

    \[\max\{|x|,|y|\}=1\]

となります。

実は\maxを足し算のように扱う数学が存在します。これをトロピカル代数といいます。
そして、実はx^{2n}+y^{2n}=1の極限を実際に考えるとこの式に帰着されるのです。これについてはまた今度書きます。

円と正方形の関係はこのようになっています。その背景には実は最先端の数学があったのでした。

この記事を書いたブロガー

sato
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

前の記事

円と定規さえあれば正多角形が書ける話

次の記事

「時間感覚」と「自分のイメージ」が曖昧な私の世界