こんばんは、satoです。
目次 非表示
はじめに…
この記事では専門的な数学の話をします。
どちらかといえば「数学に興味がある」とか「数学を勉強している」人向けになります。
その辺りをご了承くださいませ(;’∀’)
今日の話は「微分方程式をどうやって解くのか?」ということについて、よく書かれている公式がどうして成り立つのかを考えてみたことをまとめてみました。
その中で「接続」という概念も出てくるので、その解説をします。
微分方程式の解法
たとえば、次の微分方程式を考えます。
![]()
このように方程式の中で高々2階微分で表されるものを2階微分方程式と言います。
2階微分すると
これ、答えは
教科書によくある解法
大学一年生とかで習う解法は次のようになります。
まず方程式を![]() とすると、
とすると、![]() を
を![]() に置き換えてできる
に置き換えてできる![]() を解くと
を解くと![]() となります。
となります。
これを使うと微分方程式の解が![]() となります。ただし、
となります。ただし、![]() は任意の定数です。
は任意の定数です。
ここで、オイラーの公式![]() を用いると
を用いると
![]()
となり、
この解法の中で一つ方程式を解いたところがありますが、これを「特性方程式」と言います。
特性方程式を解いたら、その解から微分方程式の解が解けてしまうのです。
もう少し詳しく
ところで、どうしてこのように解答できるのでしょうか?それは次のような計算をしているからです。
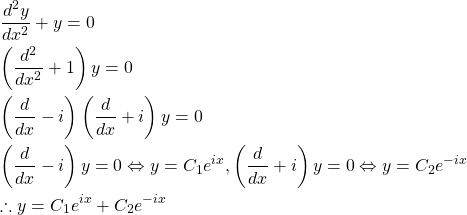
最後の方程式は「微分すると![]() が出てくる関数」ということで簡単に求められます。
が出てくる関数」ということで簡単に求められます。
特性方程式は「微分方程式を因数分解」するために使ったわけです。
また、最後の話は「重ね合わせの原理」というものを使っています。先ほどの簡単な微分方程式を満たす二つの解はどちらも、元々の微分方程式の解を満たします。
ここから、二つの解を足し合わせたものも解となるというのが重ね合わせの原理なのです。
特性方程式が重解を持つ場合
こうして、2階微分方程式を解けるのですが、この解法には問題が一つありまして…特性方程式が重解を持つ時にうまく行かないということです。
![]()
の特性方程式は
![]()
と一つの解しか出てきません。こういうとき教科書には二つ目の解として
が…どうしてこの解が出てきたのでしょうか?
疑問
そもそも、特性方程式がどうして出てきたのか?特性方程式と微分方程式にはどういう関係があるのか?
また、重ね合わせの原理がどうして成り立つのか?
など、いろいろ疑問が出てきます。今日はこれについて自分なりに理解したことをまとめてみます。
行列の話が分かればある程度は分かるはず。大学一年生の線形代数の知識を前提としています。
微分方程式を行列で表す
というのが、これから話す解き方のコンセプトです。
記号の解説
二つの関数![]() があったときに、
があったときに、
![]()
というように2つの関数によるベクトルを考えます。そして、このベクトルに関して
![]()
というようなベクトルに対する作用素を定義します。ようするに
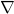 を行列で表す
を行列で表す
さて、今
![]()
を満たすような関数
微分方程式から
![]()
が成り立ちます。最初は当たり前、二番目の式は微分方程式の言いかえです。
これを使うと
![Rendered by QuickLaTeX.com \[\nabla\begin{pmatrix}y \\y'\end{pmatrix}=\begin{pmatrix}\frac{dy}{dx} \\\frac{dy'}{dx}\end{pmatrix}=\begin{pmatrix}0&1 \\-1&0\end{pmatrix}\begin{pmatrix}y\\y'\end{pmatrix}\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-ba1f01cd1d4c2317b34c3a8105321f78_l3.png)
となります。
ここまで何をしたかと言いますと微分方程式を満たす関数とその導関数の組が![]() がどのように変換されるかを行列で表現したというわけです。
がどのように変換されるかを行列で表現したというわけです。
行列と言えば…
大学一年生の時に「固有値」を嫌というほど計算させられたと思います。というわけで、さっき出てきた行列(![]() とします)の固有値を求めましょう。
とします)の固有値を求めましょう。![]() なので、
なので、![]() となります。(
となります。(![]() は単位行列)
は単位行列)
ここで「特性方程式」が出てきましたね!
さて、ついでに固有ベクトルを求めますと![]() のときは
のときは
![]()
、
![]()
となります。ここで
![]()
と置くと、
![]()
が成り立ちます。対角化ですね。ここから
![]()
となります。
微分方程式を変形する
さて、上を用いると
![]()
となります。ここで、ベクトル
![]()
とすると、
![]()
となります。つまり、
![]()
となるのです!この方程式から
![]()
が得られるので、あとは
いやー長かったですね…。
で、結局何をしたの?
先ほどの解法に比べると分かりにくいし面倒くさい気がするこの「微分方程式を行列に置き換える」という解法ですが、結局何をしたのでしょうか?まとめると
与えられた微分方程式の解とその導関数の組によるベクトルを、![]() という作用がどのように変換するのかを考えます。
という作用がどのように変換するのかを考えます。
そうして、![]() という変換によって動かない固有ベクトルを求めます。すると、この組に対しては微分方程式が簡単になります。
という変換によって動かない固有ベクトルを求めます。すると、この組に対しては微分方程式が簡単になります。
その簡単な微分方程式を解くことで元の微分方程式の解を得ました。
という流れです。で、この![]() というのが接続と言われているものです。微分方程式とその導関数の組は一つの「幾何学」的なものがあるのですが、その間の変換を表しています。
というのが接続と言われているものです。微分方程式とその導関数の組は一つの「幾何学」的なものがあるのですが、その間の変換を表しています。
で、その行列での表現を「接続行列」と言ったりします。
長いようですが、一つ一つの変形がどのようになっているのかをより深く理解できます。
特性方程式は接続行列の固有方程式
微分方程式の因数分解の正体は固有ベクトルによる![]() での変換
での変換
重ね合わせの原理は固有ベクトルから元の微分方程式の解を出す計算
に対応しているわけです。
さらに、特性方程式の解が重解の時にどうして二つ目の解がああなるのかについても説明できます。
特性方程式が重解を持つ場合
![]()
上と同様に
![]()
とすると、微分方程式の解とその導関数の組からなるベクトルに対して
![]()
となります。ここで出てきた行列を
この固有ベクトルを求めると
![]()
の一種類だけになります。あれ、これだと対角化できないぞ…(;’∀’)
広義固有ベクトル
そこで、広義固有ベクトルというものを使います。固有ベクトルは![]() となるベクトルですが、広義な固有ベクトルというのは適当な自然数
となるベクトルですが、広義な固有ベクトルというのは適当な自然数![]() に対して
に対して![]() となるベクトルを表します。
となるベクトルを表します。
求めるときには固有ベクトル![]() を使って
を使って![]() となる
となる![]() を求めて、あとは順次…という流れです。
を求めて、あとは順次…という流れです。
この場合は計算すると、たとえば
![]()
が当てはまります。さらに、
![]()
とすると、次が成り立ちます。
![]()
このように、対角化できない行列も上三角行列に変えることができます。
微分方程式を変形
これを用いると
![]()
が成り立ちます。よって、ベクトル
![]()
とすると、
![]()
となります。
これで、
![]()
という微分方程式が得られました。このうち二番目はすぐに計算できて
非線形微分方程式
さて、これを使うと一つ目の微分方程式が
![]()
となりますが、これは実を言いますと非線形微分方程式というものになります。今まで扱っていた「線形微分方程式」と違って、これを解くことは簡単ではありません。
この場合は![]() が解になります。これを「特殊解」と言います。実際にこれを求めるときにはラプラス変換とかを使えばいいのですが…私はまだ理解できてません(´・ω・`)
が解になります。これを「特殊解」と言います。実際にこれを求めるときにはラプラス変換とかを使えばいいのですが…私はまだ理解できてません(´・ω・`)
というわけで、一つ目の微分方程式の解は![]() となりました。
となりました。![]() であることからこれが元の微分方程式の解となるわけです。
であることからこれが元の微分方程式の解となるわけです。
つまり、重解の時に出てくるもう一つの解の正体はこの非線形微分方程式の特殊解だったのでした。
まとめ
というわけで、2階線形微分方程式の解法を詳しく考えてみた結果を書きました。
まとめると、微分方程式を「接続」という概念を通して行列に置き換えて、固有方程式を解くことで固有値を求め簡単な形に帰着させるということでした。
ちなみに、微分方程式とその導関数の組は一つの「幾何学」的なものと書いた話は正確に表現しようとすると「![]() -加群」の話に繋がります。
-加群」の話に繋がります。![]() とは微分作用素環のことです。
とは微分作用素環のことです。
ただ数式を当てはめるだけで解ける微分方程式。
だけど、その解法の奥底には線型代数の理論を駆使した世界、そして幾何学の世界があるのです。
このように、御言葉も奥深い世界があります。単に言葉だけ見るとなにも分からないですが、その奥にある霊の世界を見ると…とても深い次元の言葉だとわかるのです。
…初めて数式を交えた専門的な記事を書きましたが、とても長くなりましたね(;’∀’)ここまで読んでいただきありがとうございました。
今後もこういう研究メモを書いてみようと思うので、数学好きの方はチェックしてみてください(*‘∀‘)
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件


