【数学小説】真理の森の数学セミナー～分数と割り算①～

SHARE

→序章③

「さて、どこから始めましょうか」

黒板の前に立ち、3人に向き合う真理。

「そうね、まずは『比』の話からにしましょう」

しばしの黙考の後、小声でそう話すと彼女は2つの円を黒板に書いた。

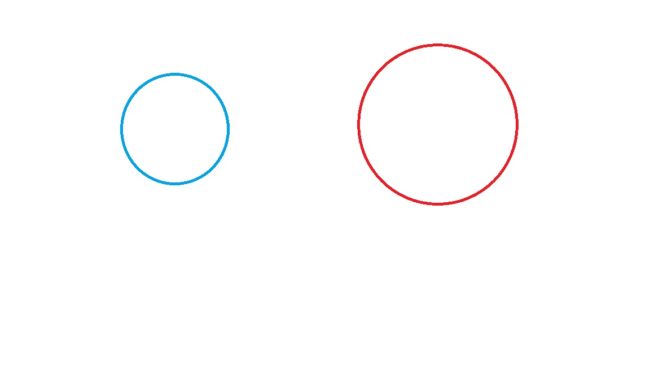
そして、座っている3人の方に向かって質問した。

「この2つの円、どちらのほうが大きいかしら？」

その質問に、ディーが答えた。

「…見たまんまで良いんだよな？
そんなの、右側の方が大きいに決まってるだろ」

「ええ、その通り。
じゃあ…」

真理は2つの円を交互に指差しながら続ける。

「右側の円は、左側の円よりどれくらい大きいかしら？」

「それは…」

ディーはしばし考え、

「答えられねぇよ、比べようがないじゃないか」

と匙を投げる。

「それもそうね。じゃあ…」



「円の数にしましょう。右と左、どちらがどれくらい多いかしら？」

新たな質問に、ディーは即答する。

「右の方が多いな。3つ分」

「へぇ…」

ディーの答えを聞いて、真理はかすかに驚いたような反応をした。
そして、俯きながらしばし考える。

「…そう考えるのね」

「…おい、どうしたんだ？」

「…あぁ」

ディーの言葉を聞いた真理は、彼の方に向き直って続けた。

「ごめんなさい、少し考え事をしていたの。
ディーの言うことは正しいわ。
だけど、ここでは”右側は左側の何倍か”で考えましょう」

「どうしてなんだ？」

質問するディー。

「そうね…。たとえば、次の2つを比べましょう」

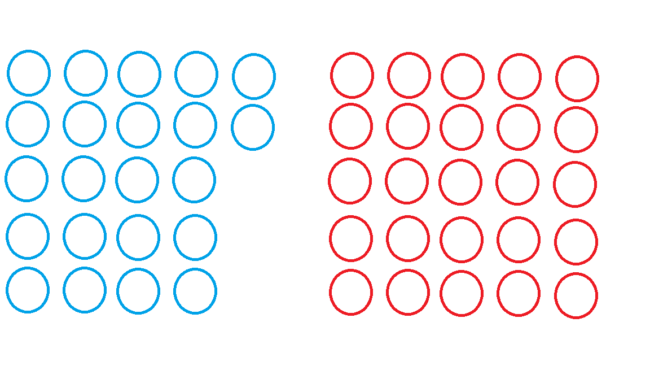
「最初の例は右が6個で左が3個。
この例は右が25個で左が22個。どちらも3つだけ増えたわね。
ところで、この2つを比べた時、同じように増えているように感じるかしら？」

真理の話を聞いて、3人はしばし黒板に書かれている図に注目する。

「う～ん、なんか最初の方がたくさん増えているように感じるなぁ」

真理の質問に答えたのはアキだった。

「確かに、そうだな…。
同じ3つだけ増えているはずなのに、下の方はそこまで増えていない気がするぜ」

「そう。同じ数を加えたとしても、2つの数を比べた時にたくさん増えているように感じることもあれば、そこまで増えていないように感じることもある。
この感覚を正確に掴むのが、”比”なのよ」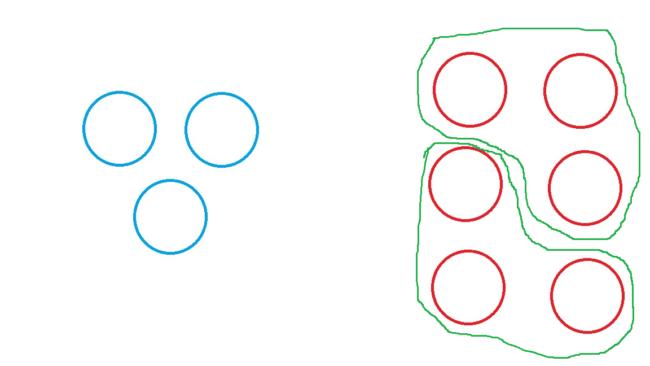

「たとえば最初の例では、右側の中に3が2つ分あるでしょう。
これが右側は左側の2倍というわけ」

「じゃあ、右は左の2倍大きい、ってわけか」

「ええ。
このように2つの対象…数を比較して、その数の変化率を表したものを”比”と言うのよ」

「2つのものを比べるから、”比”って言うんだね…」

そう話したのは、アキだった。彼女はどうやら比という言葉に反応したようだった。

「ん、でもよ。
2つのものを比べるって言ったって”右側と左側”どっちを比べるんだ？」

一方、ディーの方は疑問が思い浮かぶ。

「え、どういうこと？」

「…いや、今の3と6の場合だったら6は3より大きいけど、3は6より小さいだろ？
それをどうやって区別するんだ？」

「へぇ…いいところに気づくわね」

その疑問に対して、真理が感心したように呟いた。

「確かに6と3を比べるにしても、どちらを基準とするのかによって結果が変わるわね。
そこで、比の書き方のルールを決めましょう」

    \[6:3\]

「こう書いた時は、右側を基準にして、左側を比較していることにするわ」

「なるほど、じゃあこの場合は3を基準にして6がどれくらい大きくなったのかを比較してんだな」

「その通りよ。
そして、この場合だと”6は3の2倍”だけど、この”2倍”というのが”比の値”というものなのよ」

「比の値…」

「ええ。今の言い方だと”比で表される2つの数の変化率”を表したものが比の値ね。
…ここまでは良いかしら？」

真理が話を一区切りして、前に向き直る。

そこで

「…ん～、一番最初の丸の大きさなんだけど…
私はなんとか比べられそうな気がするなぁ」

とアキが話した。

「ん？そうなのか？」

「正確にどれくらい…というのは分からないけど、左側の丸がどれくらい右側の丸に入るのかを見たらいいんじゃないかな」

と言いながら、アキは黒板に向かい

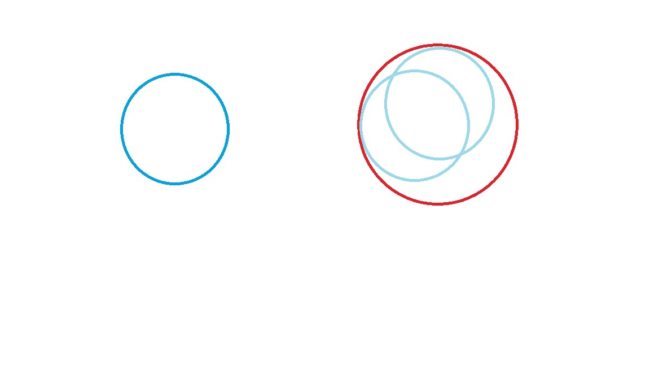
黒板の左側の円と同じ大きさの円を、右側の円の中にいくつか描いていった。

「…うーん、こうやって書くと意外と少ないんだね。
一個は入るけど、二個分はあるかないか…くらい？」

そういって、真理の方を見た。

「そうね。今アキがやったように、”2つのものを比べるときに、片方がもう片方の何個分か？”を見ていくのが、比の基本的な考えね」

「そっか！間違っていなくてよかったぁ」

とアキは安心したように話し、トコトコと机に戻った。

「…さっきから聞いていたけど、アキもディーも数学のセンスはあると私は感じるわ」

「え！？そうかな？」

「ホントかよ…」

真理の意外な言葉に、アキは喜び、ディーは訝しげである。

「…計算ができるとか、できないとかじゃなくて、ディーは疑問を持つところが良いのよ。当たり前に感じるけれど、見落としそうなところを気にする感じね。
アキは発想が柔軟だわ」

「えへへ…」

褒める言葉に照れるように微笑むアキ。

「…」

一方、ディーはその言葉に対してまだ実感がわかないようだった。

「続けましょうか。
今のアキが言うように、右側の丸はどうやら左側の丸1つは入りそうだけど、2つは入らなさそうね。
すると、右側は左側より大きいから比の値は1より大きい。一方、2倍でもない」

「このような自然数では表せない比の値を表すのが、分数よ」

この記事を書いたブロガー

sato
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

前の記事

北海道胆振東部地震から2年～生きることへの感謝～

次の記事

世の中の刺激は強すぎる