統計に出てくる『確率分布』って何だろう？離散編 | 摂理研究所/キリスト教福音宣教会

おはようございます、satoです。
この記事はtsujimotterさん主催の日曜数学 Advent Calendar 2021 の8日目の記事になります。
前日はにせいさんによる数学が好きな人を好きな人のための数学基礎知識でございます。
私も仕事柄「数学を人に教える」ことが多いのですが、その視点で見てもとても(数学専門の人にも、数学を知りたい人にも)ためになる記事だなと感じました。
最初の「定義」の話は確かに数学あるあるだなと思います笑

ところで、私の紹介をしてもらったのですが、「摂理発バーチャルYoutuber」と名乗っていた…(´・ω・｀)なのに全然動画を作れない…(´・ω・｀)

ということで、久々の数学記事です。

目次非表示

前段
まずは基本：確率とは
- 余談：天気予報
- 余談：実際の起こりやすさ
本編：確率分布とは
- 確率分布を関数で表す
離散から連続へ

前段

本日は、統計で出てくる『確率分布』って何だろう？というテーマで話を進めていこうと思います。
背景として、私は仕事の関係で色々な人に数学を教えているのですが、その中で統計を教えることがあります。
統計において初学者が躓きやすいポイントがたくさんありますが、その中の1つが確率分布、特に連続確率分布だというのが、現場で教えている私の感覚です。例えば正規分布というのがよく使われるわけなのですが、これがよくわからない、という言葉がよく聞かれます。

そこで、私自身の整理のために、自分が理解できている範囲で改めて『確率分布』についてまとめてみよう、というのがこの記事になります。
昨今統計学は社会においてもよく使われる分野で、多くの人が勉強、ないしは実用しているものと思われます。
少しでもこの記事が確率分布の理解の助けにつながればという気持ちで書かせていただきます。

(内容は数学的事実に基づいていますが、私の主観・感覚の部分もあります。数学的ミスがありましたらツッコんでいただけると幸いです)

まずは基本：確率とは

『確率分布』という言葉は『確率』と『分布』の2つに分かれます。
そういうわけで、まずは『確率』とは何かを振り返ってみましょう。

確率とはある事柄に対して、「それがどれくらい起こりやすいのか」を数値化したものと考えられます。
『必ず起こらない』ときを $0$ 、『必ず起こる』ときを $1$ としたときに、 $0$ と $1$ の間の数で起こりやすさを表現します。起こる可能性が高いほど $1$ に近い、というわけです。

では、これをどのように計算するのか、というと…例えば、「6面サイコロを1つ振ったときに、1が出る確率」を計算したいとします。この時、次のように計算します。

サイコロを振ったときに出る目は1,2,3,4,5,6の $6$ 通りである。このうち1の目が出るのは $1$ 通りなので、 $\frac{1}{6}$ である

このように、「ある行動をした(今の場合は『6面サイコロを1つ振る』、これを試行と言います)とき、その結果全ての場合の数に対する自分が知りたい現象の場合の数の割合」で計算します。言い換えると「起こりうる結果全体に対するその現象の割合」が確率です。

ただし、このような計算をする場合には一つ一つの結果が同じくらいの割合で起こるということが条件となります。先のサイコロの例でいうと、「サイコロが歪んでいるとか、6の目がやたら重い(重心が傾いているので1が出やすい)」と計算が合いません。

このあたりは中学生以上だと聞いたことがあるという人が多いのかなと思います。

なお、この確率の定義は「古典的確率論」と呼ばれるもので、これとは別に「確率が満たすべき性質」を定義として、その定義から何が分かるのかを考える「公理的確率論」というものもあります。こっちについても結構大事なのですが、今回は省略します。

余談：天気予報

これは余談ですが、天気予報に出てくる降水確率もこのような計算になります。
最初に確率を勉強した人は「雨が降るか降らないか」の $\frac{1}{2}$ なのではないか、と考えるかもしれませんが、これは「雨が降る」と「雨が降らない」が同様に起こるかどうかがわからないので(これを数値化したのが降水確率です)不適切です。

降水確率はその時点での気象条件が100回あったときに、何回雨が降っているのかという方法で計算しています。つまり、過去の事象を参考にして計算しているわけです。
(詳しくはこちら
知っているようで知らない話：降水確率50%ってつまりどういう意味？
降水確率30%…傘はどうする？数字に隠れた「雨のサイン」)

この場合は「現在の気象条件と同じ時の天気全体」のうち「雨が降っている」割合が降水確率、というわけです。

ちなみに、「降水確率はそのエリア全体のうち雨が降っている割合」というのは間違いなのだそうです。…私これを書こうとしていたのですが、ふとちゃんと確認しようと思って

余談：実際の起こりやすさ

また先程書いたように、中学校で習う計算には「同様に確からしい」という条件、つまり「それぞれの結果が同確率で起こる」が必要となりますが、実際に各場合がどれくらいの割合で起こるのかは「同じ試行を何回も繰り返し、そのうち自分が知りたい現象が何回起こったのかを調べる」ことでわかります。これは「統計的確率」と呼ばれます。

試行回数を増やせば増やすほど、「その現象の持つ起こりやすさ」と一致する、というのが大数の法則として知られています。たとえば、 $6$ 面サイコロを1回振る、という試行を何回も繰り返すと、そのうち1の目が出る回数の割合は $\frac{1}{6}$ に近くなっていきます。

これについては、こちらの記事も参照ください。

大数の法則を通して神様が摂理人に語られたこと

本編：確率分布とは

確率について振り返ったところで『確率分布』の説明に入ります。

たとえば、『コイントスを4回して表の面が何回出るか？』という問題を考えます。

表の面が出る回数は0,1,2,3,4回のいずれかになります。それぞれの確率は、

$0$ 回が $\frac{1}{16}$

$1$ 回が $\frac{4}{16}=\frac{1}{4}$

$2$ 回が $\frac{6}{16}=\frac{3}{8}$

$3$ 回が $\frac{4}{16}=\frac{1}{4}$

$4$ 回が $\frac{1}{16}$

となります。この結果をグラフにすると、次のような形になります。

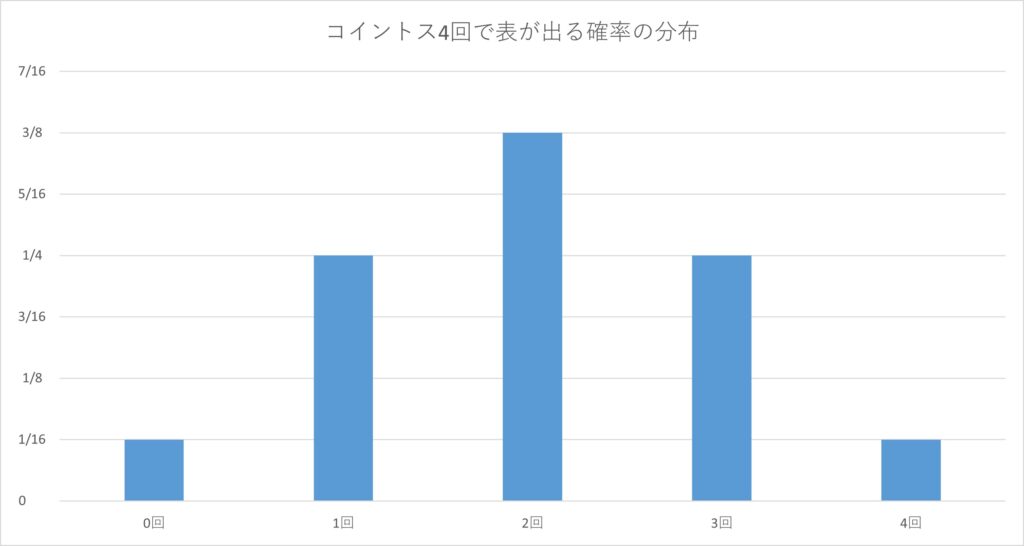
これを見ると、表が出る確率が2回である割合が全体の中で一番多いな、とか、全体で見ると左右対称なんだな、とか、色々なことがわかります。

さらに、これを見ると、たとえば『表が2回以上出る確率』というのも簡単に求めることができます。具体的には

$\frac{3}{8}+\frac{1}{4}+\frac{1}{16}=\frac{11}{16}$

と2,3,4回の確率を足すことで、2回以上表が出る確率が $\frac{11}{16}$ と求められます。

このように『確率分布』とは1つの試行に対して起こる結果の確率をまとめたものになります。

確率分布を関数で表す

実際の『確率分布』の定義は…確率変数を定義して、ある集合に対して「確率変数が集合に属する確率」を出す関数です。

先程の例で言うと、確率変数 $X$ は「表が出る回数」にあたり、確率分布を $P$ としたときに $P(X=1)$ で『コイントスを4回して表が1回だけ出る確率』を表します。これは上のグラフから $\frac{1}{4}$ となるので、

$P(X=1)=\frac{1}{4}$

となります。なお、 $X=1$ は $X\in \{1\}$ に該当します。

また、 $P(2\le X)$ で『コイントスを $4$ 回やって2回以上表が出る確率』を表します。これは先程の計算から $\frac{11}{16}$ となるので、

$P(2\le X)=\frac{11}{16}$

となります。 $2\le X$ は $X\in \{x|2\le x\}$ に該当します。この場合、 $X=2,3,4$ 以外のXになることはないので

$P(2\le X)=P(X\in \{2,3,4\})$

と同じです。

離散から連続へ

さて、一番最後の話でもあったように、『コイントスを4回やって表が出る回数』は $0,1,2,3,4$ のいずれかでした。特に分数や小数にはなりません(1/2回とか0.3回とかは考えられませんよね)。
この「回数」とか「個数」みたいに、値が自然数(0を含む)、または整数になるような量のことを「離散量」、このような量を横軸とする確率分布を離散確率分布といいます。