おはようございます、satoです。
目次 非表示
地球は「丸い」けど「平ら」
今週摂理の御言葉で伝えられた中にこんな話がありました。
私たちが住んでいる地球はボールのように「球」でできています。それなのに数十里行っても「平地」です。だから住みやすく、行き来しやすいです。-鄭明析先生の主日礼拝の御言葉「次元を上げて実践しなさい」より
確かに、私達が平素生活している中で地球が「球状」であることを意識することってあまりないと思います。
あるとしたら、飛行機での移動中とか、宇宙に行った時くらいでしょうか?
数学的にいうと、これは「地球(2次元球面)は接平面を定められる」ということです。
接平面というのは文字通り、図形のある点に接している面のことです。
簡単に言うと「全体としては丸いけど、小さい部分は平面と同じ」ってことです。それくらい滑らかな図形なんですね。
ちなみに、微分積分の言葉でいうと、球面は至る所で全微分可能であるといいます。
難しい話はこのくらいにして(笑)
ところで、どうして私達が生活している時には「平地」のように感じられるのでしょうか?
それは次のように御言葉で話されていました。
どうして地球は「球」なのに「平地」でしょうか?それだけ大きいからです。
-鄭明析先生の主日礼拝の御言葉「次元を上げて実践しなさい」より
球の半径が大きいほど、カーブが緩やかになります。これは自動車を運転するときにも大事な話です。
もし地球の半径が小さいと家を立てるときにも不便です。基本木や石はまっすぐなのに、カーブに合わせて建てなければならないから、加工も大変ですし、支えるときも不安定になります。
もっと小さいと、立っているときも不安定になります(よくサーカスにいる玉乗り少年を考えてみると分かります)
このように、私達の考えのスケールを大きくしてこそもっと楽で住みやすい、違った世界になります。
というのが鄭明析先生がおっしゃりたかったことです。
果たしてどれくらいのスケールなの?
さて、「それだけ大きいから」と話してましたが、具体的にどれくらい大きいと地球が球なのに平地になるのでしょうか?
このあたり、数学者として見逃せない(笑)ちょっと具体的に考えてみることにしました。
問題をどのように定義するかで、この結果が変わってきます。
ここでは問題を次のように考えます。
まず、私たちの平均身長は1.5mくらいでしょう。そんな私たちが生活する中で「1mmの誤差」はあまり気になりません。というか感じられない人がほとんどです(笑)
また、家を建てるときにも1mm以下の誤差は無視しても…大丈夫なのでしょうか?ここは自信ありません(ノД`)
そして、私たちが生活する中で起点となるのは家ですが、家は高々半径100m以内に収まる大きさであるとします。それを越えるのはたぶんトランプ大統領のような大富豪の家くらいだと思われます…(*´・ω・)(・ω・`*)
というわけで、ここでは「自分を中心として半径100m以内の位置に対して、接平面と球面の差が1mm以下なら平面だとみなせる」とします。さて、この時地球の半径はどれくらいならちょうどいいのでしょうか?
ここからいくつか数式を出したいと思います。なお、これ以降単位はkmで統一します。
まず、半径![]() kmの球面の方程式は
kmの球面の方程式は![]() です。ここで、自分が球面の頂点に立っていると仮定します。
です。ここで、自分が球面の頂点に立っていると仮定します。
すると、接平面は![]() です。一方、半径100m=0.1kmの位置、というのは
です。一方、半径100m=0.1kmの位置、というのは![]() ということを表します。よって、この時の
ということを表します。よって、この時の![]() は
は![]() となります。この2つの差、つまり
となります。この2つの差、つまり
![]()
が1mm=![]() 未満となる
未満となる![]() を求めよ、という問題になるのです。
を求めよ、という問題になるのです。
計算すると…
試しに地球の半径6371kmを![]() としてみました。すると…
としてみました。すると…
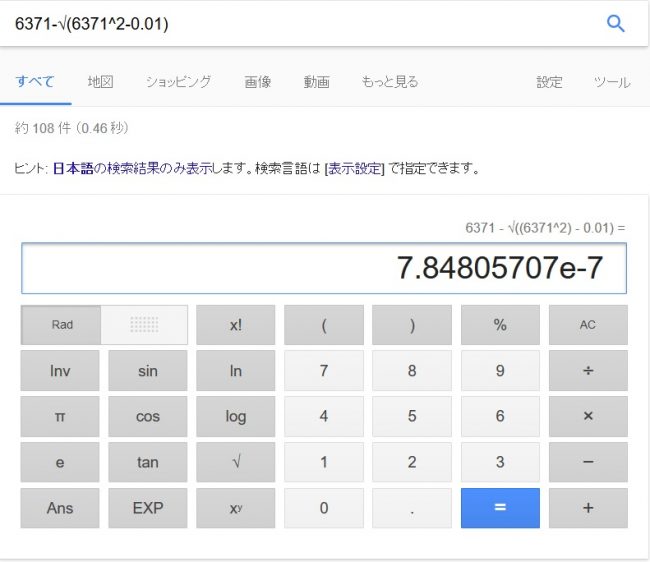
約![]() と出ました!確かに条件を満たしていますね…!
と出ました!確かに条件を満たしていますね…!
調べてみると5000km以上なら誤差が1mm以下となります。
実際の生活での感覚と計算が一致しました!
このように計算で確かめられるのが数学の良さ。
建築の専門家的には1mmだと微妙なのかもしれませんが、ちゃんと人間の生活のスケールに合わせて地球を適切に創造された、というところに神様の絶妙さを確かめることができました( ´∀`)
本当に感謝します~( ´∀`)
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件