最近考えた数学の話：層の射について | 摂理研究所/キリスト教福音宣教会

おはようございます、satoです。
この頃ブログを結構書いていますが、最近数学の話を全然してないですよね。
「摂理研究所」って名前なのに…聖書の研究はたくさん書いてますね笑笑
私の研究スタイルとして様々なことを実践によって確認し、それを分析することで理解していくというものがあります。
信仰もこのスタイルでして、色々なことを試してみながら、より自分に合った信仰生活を模索している段階です。

私の仕事の一つにして、最も大きなウェイトを占めるのが「数学研究」です。これは趣味も兼ねていまして(笑)、私は時間が空くと数学をしたり、考えたり、ネットを見たりしています。(ネットは数学に関係ないものも含む)
今日はある数学の問題を考えた時に面白かったことがあったので、それを書きたいと思います。

なお、今日の内容は完全に数学ネタです。専門的な内容であることにご留意ください。

目次非表示

層の射は層の構造を保つのか？
証明
感想

層の射は層の構造を保つのか？

数学には「層」という概念があります。
これは位相空間 $X$ に対して定義される数学的対象で、最先端の数学において議論の土台となる道具の一つです。
以下に、その定義を書いていきます。

$F$ が位相空間 $X$ 上の層である、というのは、 $X$ の開集合ごとに「集合」があって、それが綺麗につながっている、というような対象です。
これを数式で表現すると次のようになります。

まず $F$ として次のような組を考えます。
・ $X$ の開集合 $U$ ごとに定められた集合 $F(U)$
・ $X$ の開集合 $U, V$ が $V\subset U$ となる時、次の(1), (2)を満たす写像 $\rho_{U, V}^F:\ F(U)\rightarrow F(V)$
(1) $\rho_{U,U}^F:\ F(U)\rightarrow F(U)$ は恒等写像
(2) $W\subset V\subset U$ となっている時、 $\rho_{V,W}^F \circ\rho_{U,V}^F = \rho_{U,W}^F$
以上を満たす組 $(F,\ \rho^F)$ (もう少し言うと、位相空間 $X$ から導かれる開集合の圏 $T(X)$ から集合の圏への反変関手)を $X$ 上の前層と言います。

さらに、前層 $F$ が条件[Ⅰ]、[Ⅱ]を満たしている時にX上の層といいます。

[Ⅰ] 開集合 $U_\lambda\subset X\ (\lambda\in\Lambda)$ に対して $U=\bigcup_{\lambda\in\Lambda}U_\lambda$ とする。
$s,\ t\in\ F(U)$ が、任意の $\lambda\in\Lambda$ に対して $\rho_{U,U_\lambda}^F(s)=\rho_{U,U_\lambda}^F(t)$ が成り立つならば $s=t$ である。

[Ⅱ] 開集合 $U_1,\ U_2\subset X$ に対して $U=U_1\cup U_2$ とする。
$s_i\in F(U_i)\ (i=1,2)$ が $\rho_{U_1,U_1\cap U_2}^F(s_1)=\rho_{U_2,U_1\cap U_2}^F(s_2)$ を満たすならば、ある $s\in F(U)$ が存在して、 $\rho_{U,U_i}^F(s)=s_i$ が成り立つ。

[Ⅰ]は「部分を調べて全部同じなら、全体として同じ」ということを、[Ⅱ]は「部分同士を張り合わせられる」ということを表しているのかな、と考えています。

さらに、2つのX上の層 $F,\ G$ に対して、層の射 $\phi: F\rightarrow G$ を
$X$ 上の開集合 $U$ に対して、(a)を満たすような写像 $\phi_U: F(U)\rightarrow G(U)$ の組
(a) $V\subset U$ となるX上の開集合 $U, V$ に対して、 $\rho_{U,V}^G \circ \phi_U=\phi_V \circ \rho_{U,V}^F$
とします。

実はこの層の射は $F,\ G$ が前層であっても定義することができます。
そこで浮かんだのが、見出しにある「層の射は層の構造を保つのか？」という疑問です。
この疑問を数式を使って具体的に表しますと

開集合 $U_1,\ U_2\subset X$ に対して $U=U_1\cup U_2$ とおく。
$s_i\in F(U_i)\ (i=1,2)$ が $\rho_{U_1,U_1\cap U_2}^F(s_1)=\rho_{U_2,U_1\cap U_2}^F(s_2)$ が成り立つとする。
このとき、[Ⅱ]よりある $s\in F(U)$ が存在して、 $\rho_{U,U_i}^F(s)=s_i$ が成り立つ。
ここで問題。
(1) $s\in F(U)$ を層の射 $\phi: F\rightarrow G$ で移したもの $\phi_U(s)\in G(U)$ に対して $\rho_{U,U_i}^G(\phi_U(s))=\phi_{U_i}(s_i)$ が成り立つか？

(2) $\rho_{U_1,U_1\cap U_2}^F(s_1)=\rho_{U_2,U_1\cap U_2}^F(s_2)$ から
$\rho_{U_1,U_1\cap U_2}^G(\phi_{U_1}(s_1))=\rho_{U_2,U_1\cap U_2}^G(\phi_{U_2}(s_2))$ が成り立つので、層 $G$ で[Ⅱ]の条件を用いると $s'\inG(U)$ で $\rho_{U,U_i}^G(s')=\phi_{U_i}(s_i)$ を満たすものが得られる。
この時、 $s'=\phi_U(s)$ が成り立つか？

(1)は「層の射は制限を保つか」、(2)は「各部分を移した時、移した部分の張り合わせは大本の移したものと一致するか」という問題です。
「層の射によって一部を張り合わせた時に、その張り合わせが保たれるのか」ということを知りたかったので、このような問題を考えました。

証明

さて、こちらの二問はどちらも成り立ちます。以下、証明です。

(1) 層の射の条件(a)より

$\rho_{U,U_i}^G(\phi_U(s))=\phi_{U_i}(\rho_{U,U_i}^F(s))=\phi_{U_i}(s_i)$

となるので成り立つ。

(2) まず、条件が成り立つことを確かめる。

$\begin{eqnarray*}\rho_{U_1,U_1\cap U_2}^G(\phi_{U_1}(s_1))&=&\phi_{U_1\cap U_2}(\rho_{U_1,U_1\cap U_2}^F(s_1))\\&=&\phi_{U_1\cap U_2}(\rho_{U_2,U_1\cap U_2}^F(s_2))\\&=&\rho_{U_2,U_1\cap U_2}^G(\phi_{U_2}(s_2))\end{eqnarray*}$

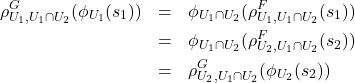
ここで、 $s'\in G(U)$ で $\rho_{U,U_i}^G(s')=\phi_{U_i}(s_i)$ となるものを取る。
(1)より $\rho_{U,U_i}^G(\phi_U(s))=\phi_{U_i}(s_i)$ が成り立つので、
$i=1,2$ に対して $\rho_{U,U_i}^G(\phi_U(s))=\rho_{U,U_i}^G(s')$ が成り立つ。
すると層の条件[Ⅰ]から $s'=\phi_U(s)$ が得られる。

以上より、層の射は構造を保つ、ということが示せた。

感想

私がこの証明をして一番面白いと思ったのは(2)の問題を考える際に条件[Ⅰ]が出てきたことです。
はじめは条件[Ⅱ]しか使わないのではないか、と考えていたのですが、貼り合わせたものが同じになるかどうかを確かめる際に使うんだな、と分かって面白かったです。
また、この問題を改めて考えてみると、意外と数式化して問題を記述するのが難しかったです。(当たり前の結果になる…ということが分かったり、そもそも何が疑問だったのか分からなくなったりしました)
現に、今回の記述で果たして私の確かめたかったことが表現できているのかは疑問が残ります。

今回の話は現在研究している内容とは異なりますが、こうやって数学の些細な問題について考えるのは割と楽しいです。
こういうことをやることで数学を含めた物事の考え方を鍛えられたり、書く練習になるので今後も時々こういう記事を書きたいなと思います。