おはようございます、satoです。
この間書いたこちらの記事がTwitterで少しだけRTされてびっくりしました(^o^)
やはり、宇宙際タイヒミュラー理論という最先端の理論を理解したい、気になる、という人が少なからずいるんだな…と。
私もその一人です。
そこで、私も少しずつ宇宙際タイヒミュラー理論がどのようなものなのかを説明している星裕一郎さんの解説論文を読みながら、そこに出てくる単語を自分なりに説明していこうと思います゚( ゚∀゚)o彡°残念ながら数論幾何は専門でないのでかなり不正確、思い込みもあるかもしれません…(´・ω:;.:…
目次 非表示
遠アーベル幾何学とは
まず、宇宙際タイヒミュラー理論につながる分野として遠アーベル幾何学があります。
これは数論幾何の一分野で、次のような哲学に基づいた理論になります。
「ある種の図形は(数論的)基本群によって決定される」
このある種の図形、というのは、「双曲的代数曲線」を含む「遠アーベル代数多様体」と言いまして、基本群が「アーベル(可換)」とは程遠い性質を持つものです。
数論的基本群というのが何かは…またいずれ…。ひとまずここで書きたいことは
「対称性を表す群から決まる図形の種類が存在する」
ということです。
この哲学を最初に考えたのはGrothendieckです。Grothendieckが挙げた12のテーマの一つで、彼が数学をしていた頃にはまだ表に上がらなかったものです。
遠アーベル幾何学についてはGrothendieck予想というものがありまして、上の哲学が「双曲的代数曲線」では成り立つということを予想しています。
これを解決したのが望月新一教授なのです。
遠アーベル幾何学の中に出てきた「群論によって性質が決まる」という考えは宇宙際タイヒミュラー理論のモデルの一つです。
望月新一教授も自身のHPにて宇宙際タイヒミュラー理論の「心」について次のように書いています。
数論幾何において本質的なのは、環やスキームのような‘具体的’な対象たちではなく、むしろそれらの具体的なスキーム論的な対象たちを統制している、様々な(‘組み合わせ論的アルゴリズム’に近い)抽象的なパターンである。
この「抽象的なパターン」が群論、あるいはモノイドと呼ばれる対象になります。
円分物
星裕一郎さんの解説論文に書かれているものの中で最初に出て来る専門的な単語が「円分物」です。
これはTate捻り![]() とのことです。…って、それは何でしょうか?
とのことです。…って、それは何でしょうか?
その次に書いてある、次の文章がとても参考になります。
(標数
の) 代数閉体
に対する
— ここで,に対して,
は,
の中の
の
乗根のなす群.
代数閉体というのを一旦複素数全体とします。(本当は![]() 進体なのだと思いますが、わかりやすくするため)
進体なのだと思いますが、わかりやすくするため)
「![]() の
の![]() 乗根全体」というのは、方程式
乗根全体」というのは、方程式![]() の解全体のことです。
の解全体のことです。
…と書いても難しいのですが、実はもっと分かりやすく話すことができます。端的に言えば…半径1の円に内接する正![]() 角形の頂点のことです。
角形の頂点のことです。
たとえば、![]() の解は、
の解は、![]() です。
です。
このときは、数直線上の![]() のところに点が打たれます。
のところに点が打たれます。
それでは![]() の解はどうなっているのか、というと、次の図のようになっています。
の解はどうなっているのか、というと、次の図のようになっています。
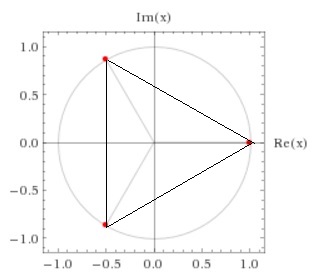
赤い点が解なのですが、これはちょうど0, 60, 120度のところにあります。つまり、![]() を一つの頂点にした「正三角形」の頂点になっています。
を一つの頂点にした「正三角形」の頂点になっています。
ちなみに、1の3乗根は![]() と書かれていますが、数学ガールでは
と書かれていますが、数学ガールでは![]() のワルツなんてものが出てきます。確かに3拍子で元に戻りますからね…。
のワルツなんてものが出てきます。確かに3拍子で元に戻りますからね…。
同様に、![]() の解は、
の解は、![]() ですが、それは複素数平面上では
ですが、それは複素数平面上では
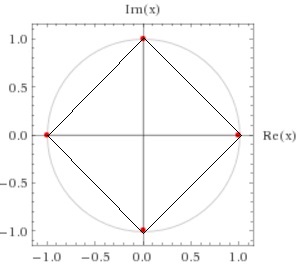
このようになります。ちょうど「正方形」の頂点になっていますね。
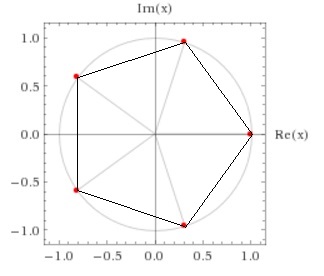
最後のは![]() の解です。これも正五角形になっています。
の解です。これも正五角形になっています。
(以上、図はWolfram alphaの計算結果を用いました。ただし、正多角形は私が編集しました。)
このように半径1の円周に内接する正![]() 角形の頂点を「集めた」ものがTate捻りの実現の一つの形なのです。
角形の頂点を「集めた」ものがTate捻りの実現の一つの形なのです。
こう考えると、Tate捻りというのは円と関わりがあるのかなと私は思いました。
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件



