「正方形が円の極限」の数学的解説

SHARE

おはようございます、satoです。

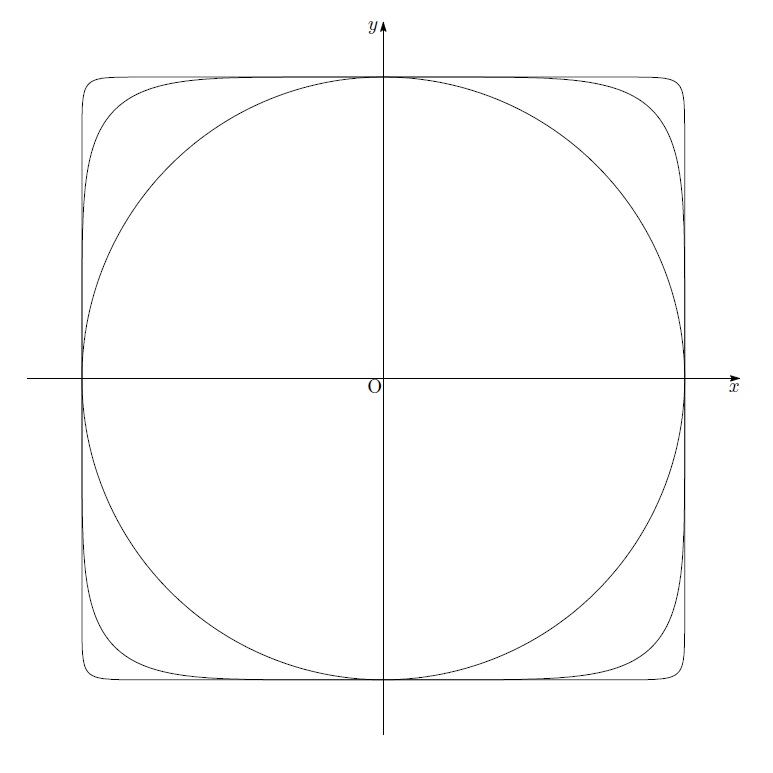
今日は前に話した「四角形が角のついた円だ」という鄭明析先生の箴言について、ちょっとした補足説明をします。

前の記事では

    \[x^{2n}+y^{2n}=1\]

のnを限りなく大きくすると、正方形の式

    \[\max\{|x|,|y|\}=1\]

となることを書きましたが、今日はこの証明をしたいと思います。

使うのは、はさみうちの原理です。理系の高校生ならなんとか理解できる話です。

目次 非表示

極限の証明

x^{2n}+y^{2n}=1は

    \[(x^{2n}+y^{2n})^{1/2n}=1\]

と同じなので、これから示すのは、次のことになります。

    \[\lim_{n\rightarrow\infty}(x^{2n}+y^{2n})^{1/2n}=\max\{|x|,|y|\}\]

では、これを示します。まず、今xもyも2乗しているので、x^{2n},\ y^{2n}は共に0以上です。
ここで、x\ge yとします。すると、x^{2n}\ge y^{2n}\ge0なので、次の不等式が成立します。

    \[(x^{2n})^{1/2n}\le(x^{2n}+y^{2n})^{1/2n}\le (2x^{2n})^{1/2n}\]

ここで、(x^{2n})^{1/2n}=\sqrt{((x^n)^2)}^{1/n}=(|x|^n)^{1/n}=|x|になります。(\sqrt{x^2}=|x|となることに注意)
そういうわけで、上の不等式は

    \[|x|\le(x^{2n}+y^{2n})^{1/2n}\le 2^{1/2n}|x|\]

となります。さらに、\lim_{n\rightarrow\infty}2^{1/2n}=1なので、不等式の両端をn\rightarrow\inftyというようにnを限りなく大きくするとどちらも|x|に収束します。
以上のことからはさみうちの原理よりx\ge yのとき

    \[\lim_{n\rightarrow\infty}(x^{2n}+y^{2n})^{1/2n}=|x|\]

となります。同様にy>xとすると

    \[\lim_{n\rightarrow\infty}(x^{2n}+y^{2n})^{1/2n}=|y|\]

になります。以上から

    \[\lim_{n\rightarrrow\infty}(x^{2n}+y^{2n})^{1/2n}=\max\{|x|,|y|\}\]

となるのでした。

ということで、「正方形が円の一種の極限になる」ということが単なる直感だけでなく、数学的にも正しいことが示されました。

この記事を書いたブロガー

sato
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

前の記事

「時間感覚」と「自分のイメージ」が曖昧な私の世界

次の記事

『守教』という本に出会って。