【数学小説】真理の森の数学セミナー～積分編⑥～

→積分編⑤

さて、どうしたものか…と数正は考えていました。

“値は分かるが積分が分からないような関数についてグラフで囲まれた面積をどう求めるか？”

これについて、数正はその方法を知っていました。
真理が言う”積分の定義”のことも。

しかし、おそらく自分が今説明したとしても…アキやディーを理解させられるか。それを数正は考えていました。
真理が「森の中」を話すとき、彼女には彼女の流れがあります。それをできる限り邪魔したくない、ということもあって彼もしばらく口を閉ざしましていました。

そうして、しばし沈黙が流れます。

「…分からん。お手上げだ」

最初に沈黙を破ったのはディーでした。
彼は両手を上げて降参のポーズを取っていました。

「それなら…少し、ヒントを出そうかしら」

そう話して、しばし天を仰ぐ真理。

「…小学校の時、三角形の面積をどう求めたか覚えてる？」

「…底辺×高さ÷2、だよな？」

「そうね。それが”どうして成り立つのか”は覚えてる？」

「えー…と…」

「確か…三角形を2つ合わせて、平行四辺形を作るんだったような…」

とアキが思い出しながら答えました。
そして、ノートに図を書いてみんなに見せました。

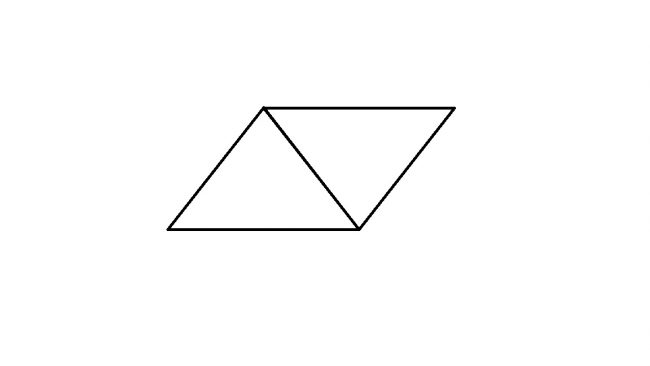
「こんな風に！」

「ええ、それで合ってるわ。
それじゃあ、平行四辺形の面積が”底辺×高さ”なのはどうして？」

「高さのところで切って…」

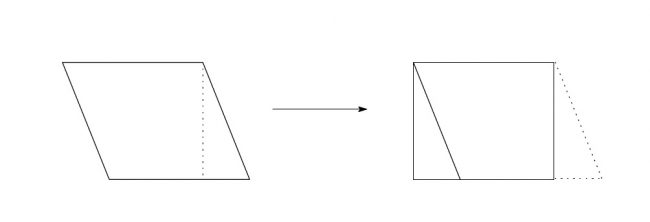
「こういう風に繋ぎ合わせると長方形になって、長方形の面積は縦×横だから？」

「その通りよ」

「すげぇ。よく覚えてるな…」

「今平行四辺形を切り貼りして”長方形に変えた”ところが一つのヒントね。ここでは長方形の面積は縦×横で求められることはOKとしましょう」

「長方形にする…そういえば、三角形の時は平行四辺形の面積を使って出してた！
これって、”分からない三角形の面積を分かっている平行四辺形の面積を使って求めた”ってこと？」

「…とても良い発想だわ。
“分からない図形の面積を分かる図形を使って求める”、これが基本的な考え方ね」

「そしたら、このグラフと直線で囲まれた図形の面積も分かっているものを使って求められるかも！」

そういって、アキはじっと黒板に書かれた図形を見つめていました。

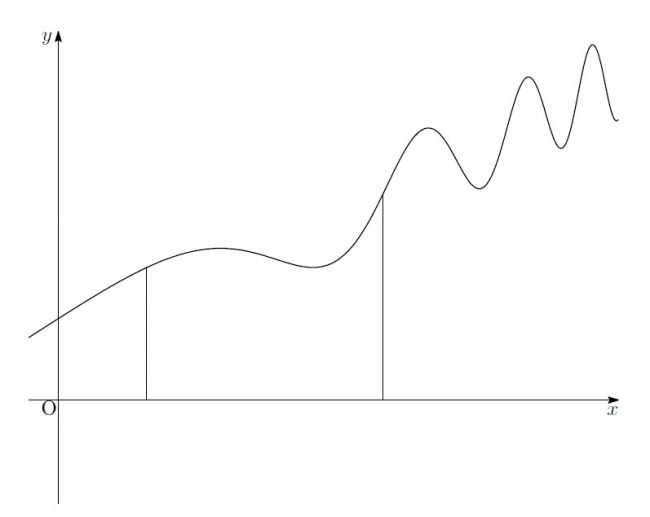
「……うーん…」

じーーっと見つめていたアキですが、

「…やっぱりわかんないなぁ」

と、目をつぶりながら言葉を出しました。
それを見た真理が再び誘導します。

「それなら、もう一つヒントを出しましょう。
“円の面積”はどのようにして求めるのかしら？」

「円の面積…半径×半径×3.14だっけ…」

「より正確にはを半径としたとき、で求められる。3.14は円周率の近似値だ」

「そうだった！でも、これってどうやって求めるんだったっけなぁ…」

「全然覚えてねぇ…」

ディーもアキも円の面積の求め方を思い出そうとしていますが、なかなか出てきません。

「これはちょっと難しいが…」

そこで、数正が助け舟を出しました。

「まず円を細かく切る」

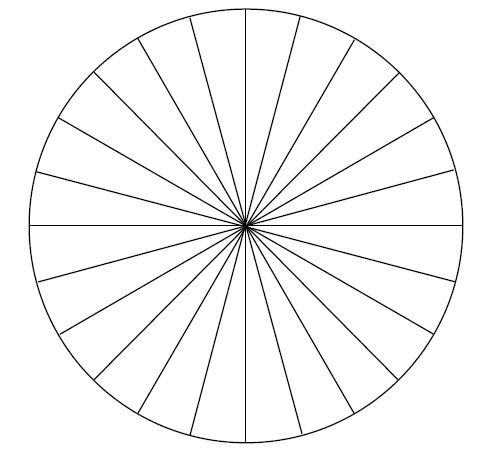
「なんだか…ピザみたい！」

「そうだな…」

アキの一言に思わずクスリとしてしまう数正。

「次に、この細かい扇形…”ピザの一欠片”をこのように並べていく」

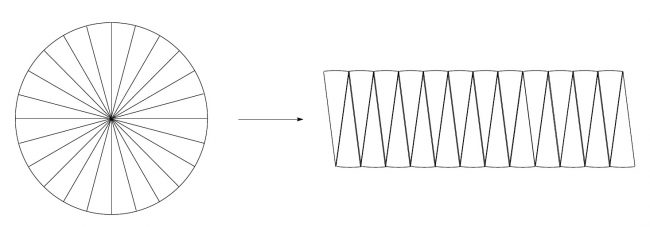
「あれ、これって…」

「平行四辺形に見えるな…」

「その通り。この扇形をもっと細かく切ると、より平行四辺形に近くなる。
今この円の半径をとすると、円周はだから、”底辺”は、”高さ”はになる。
以上から、となる」

「へぇ…」

「そういや、なんかやったことあったなぁ…」

円の面積の出し方の流れに思わずため息が漏れる二人。
真理がそのあとの説明を引き継ぎます。

「今の議論は感覚的で厳密ではないけど、今の問題についてとても重要なことを示唆しているわ。
今の円の面積の求め方は”細かくすると扇形が三角形に近くなる”というところを前提としているのよ。
もっと言うと”微小な弧は直線とみなせる”ということね」

「微小な弧…弧ってピザの縁のことだっけ？」

「そうね。扇形の縁」

「そこが、直線に…ん、ちょっと待って！」

この言葉を聞いて、アキがあることを閃きました。

「今の話って、”曲線を細かく切ると直線になる”ってことだよね？
ということは…」

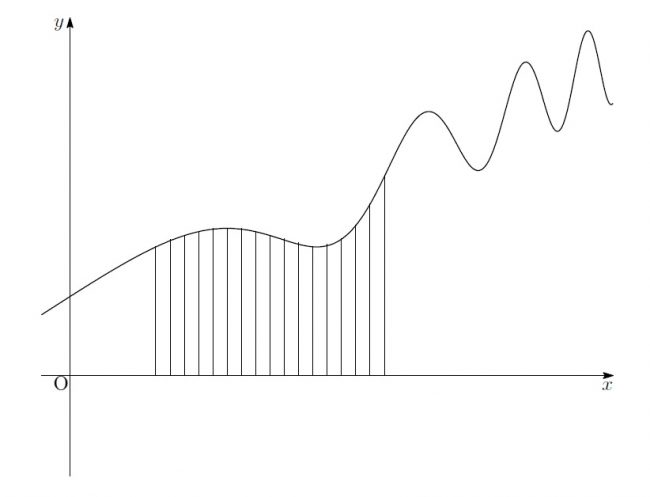
「この図形も、こうやって細かく切ったら一つのパーツは四角形に近くなる、ってこと！？」

その答えに、真理は笑顔で答えました。

「その通りよ。一つ一つは四角形、もっと言うと台形だから計算できる。
“細かく切って、一つ一つのパーツの面積を求めて、全てを足し合わせる”
これがこの図形の面積の求め方」

「なるほどなぁ…」

その答えを聞いたディーはしばし圧倒されていました。

「…しかし、”曲線を細かくすると直線になる”って話、微分でも聞いたことがあるなぁ」

ディーのそのつぶやきを聞いた真理はニヤリとしました。

「へぇ、よく覚えていたわね…。
そう、この積分の話は微分と非常に繋がりが深いのよ。この話もしたいところだけど、これは全てが終わってからにしましょうか」

とても嬉々としている真理。
彼女は深い話をすることも聞くこともとても好きなのです。

「さて、今細かく切ったパーツの面積を考えましょう。
直感的には、パーツはとても細かく切ると長方形に近くなるように見えるわ。
その高さは…」

「…横の幅は限りなくに近いから、ほぼ差はない…ということはの位置にある長方形の高さはか？」

「ええ。
この長方形の高さはに近くなる。それを足し合わせるとこの面積になる、ということ。
横の長さの合計は2つの直線間の距離になるから、その分だけ足せばいい。これを…」

「と表記する」

「…もしかして、って…”からまでの長方形を足し合わせる”ってこと？」

「そう、それを伝えたかったのよ。
ちなみに、はSを伸ばした形なのだけど、Sはsummation、合計することを意味するわ」

「そうなんだ！なんか、のことが分かってきたかも！」

「なるほど、それが”積分の定義”ってことか…」

「あれ？でも…」

とアキがあることに気づきました。

「さっき、”長方形の高さはになる”というのは分かったけど、細かく切ったら横の長さはだんだん短くなって”0に限りなく近づく”から…一個一個の面積は0になる気がするんだけど」

「言われてみりゃあ…確かにそうだ！
長方形の面積がほぼ0なら足しても0じゃねぇか！？
細かく切れば切るほど長方形に近づくけど…その面積は0になる…でも、細かく切らないと面積は分からない…いったいどうしたらいいんだ！？」

「二人の言う通りよ。
確かにこの面積の求め方は直感的には正しそうだけど、よくよく考えると”一つ一つのパーツの面積が0になる”という問題があるわ。そこで…もう少し深く考えましょう」

そう話して、真理はさらに深い森の中へと誘っていきます…。

→積分編⑦

→まとめへ戻る

この記事を書いたブロガー

sato

「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

最近の投稿

もっと見る

• 日々感じること2024年11月13日運動不足？
• 日常生活2024年11月12日最近の直さなければならないところ
• 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
• 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件