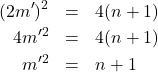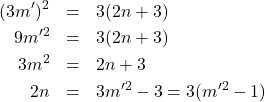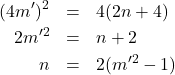【真理の森の数学セミナー】SS：原始ピタゴラス数②

SHARE


おはようございます、satoです。
引き続き『原始ピタゴラス数』をテーマにした数学小説を書きたいと思います。
前半はこちらからです。

※こちらは日曜数学 Advent Calendar 2020の13日目の記事の続きです。
(本当に書きたかったのはこっちだというのはここだけの話)

目次 非表示

2つの数の差が2となる原始ピタゴラス数

D「あー…さっきの証明、ある数と互いに素な2つの数を掛けても、その積はある数と互いに素になるってことが大事なんだな」

A「たとえば、2と3は互いに素で、2と5も互いに素だよね？そしたら、3と5を掛けた15も2と互いに素になる。これと同じ感じなんじゃないかな？」

D「互いに素の定義は『公約数が1である』ってことだったか？
15の約数は1,3,5,15だから、3の約数と5の約数、それらの積になる」

A「あとは…って、真理ちゃん何やってるの？」

二人で話し合っていたアキとディーが真理たちの方に寄ってきました。

M「今、私が考えた問題について話していたのよ。
さっき、数正が証明した問題は”2つの数の差が1になる原始ピタゴラス数”が無数に存在することを意味しているのだけど、差が2になる原始ピタゴラス数についてはどうなるのか、という問題ね」

X「その言い方だと、(3,4,5)も差が2になる2つの数が存在するように、問題がうまく成り立たない。少し言葉を付け足そう」

2つの数の差の最小が2となるような原始ピタゴラス数の存在

M「そうね。最も小さい差が2である、といえば(3,4,5)のような例が外れてうまく考えられそうね」

A「そんなことを考えたんだ…」

M「最小の差が1なら無数に存在する。
それなら、最小の差を2としたらどうなるか…と考えるのは数学にはよくあることよ」

X「フェルマーの最終定理もそうだ。
“自然数の2乗の和が別の自然数の2乗になる”ということがピタゴラスの定理なら、それを3乗、4乗と考えていったのがフェルマーの最終定理だからな」

M「そうやって新しい問題を作るのが数学の楽しみの一つよ。
…さて、そろそろ検討してみましょう。さっきの証明の右辺のn+1をn+2にするわ」

    \[m^2+n^2=(n+2)^2\]

M「それから、m<nとしましょう」

A「どうして？」

M「(4,3,5)と(3,4,5)のように、本質的に同じものを考えないようにするためね。ややこしくならないように条件を立てているのよ」

X「先ほどと同じように、n^2を移項して式変形をしてみるか」

    \[m^2=(n+2)^2-n^2=(n^2+4n+4)-n^2=4n+4=4(n+1)\]

M「右辺は偶数だから、左辺も偶数になるわね。だから、新しい文字m'を使って」

    \[m=2m'\]

M「こうしましょう」

D「待て待て！一気に進んだな…一体何をしているんだ？」

M「最初の式変形はいいでしょ？」

D「そこはさっきと同じことをしてるんだよな？
nが決まっていて、そこからmを…nを使って表そうとしてるのか？」

M「ええ、ちゃんと理解できているようね。
今m^2=4(n+1)という等式が出たけど、この右辺は偶数になっている」

D「4(n+1)は4の倍数だろ？」

M「4の倍数は2の倍数、つまり偶数でもある」

D「それはそうだが…どうして4の倍数にしないんだ？」

X「今は自然数の偶奇…偶数か奇数かに着目して話を進めている。
だから、4の倍数ではあるが、偶数として扱っているということだ」

M「こういう自然数が出てくる問題は偶奇に着目すると解きやすくなることが多いのよ。もう一つ意図があるのだけど、これはすぐに分かるわ」

D「そうなんか。それで、m^2は偶数だって分かったけど、そこからmが偶数になるのは…」

X「奇数の2乗は奇数になる。その対偶だな」

M「もし仮にmが奇数なら、奇数の2乗は奇数になるから、m^2が偶数であることに矛盾するでしょう？だから、mも偶数ってわけね」

D「なるほどな。で、数正の言っていたやつは」

X「それはすぐに計算できる。というか、さっきも同じ計算をしていた」

    \[(2l+1)^2=4l^2+4l+1=2(2l^2+2l)+1\]

A「あ、これのこと？」

X「そうだな」

M「mが偶数と分かったから、ある自然数m'を使ってm=2m'としたのよ」

D「うっし、なんとか理解したぜ。で、次は何をするんだ？」

M「m=2m'を代入しましょう」

    \begin{eqnarray*}(2m')^2&=&4(n+1)\\4m'^2&=&4(n+1)\\m'^2&=&n+1\end{eqnarray*}

A「ちょうど4で割り切れたね！」

X「さっきmを4の倍数としなかったのはこのためか」

M「ええ。2の2乗は4となるから、きれいに割り切れるのよ」

D「ってことは、n=m'^2-1か…これって互いに素になるのか？」

M「まずnとn+2が互いに素になるためには、nは奇数である必要があるわね」

A「偶数だったら、2を足しても偶数だもんね」

M「そしてn=m'^2-1とm=2m'だけど、これは…」

X「m'^2-1=(m'-1)(m'+1)で、m'とm'-1、m'とm'+1はどちらも互いに素だから、m'とnも互いに素だな」

A「さっきやった、この話！」

D「ああ、あれか。互いに素なやつを掛けても互いに素ってな」

M「最後にm'が奇数なら、n=m'^2-1は偶数になるから、互いに素でなくなる。よって、m'は偶数ね。すると、m'-1とm'+1は奇数になるから、2とnも互いに素。以上よりm'が偶数ならば、(2m',m'^2-1,m'^2+1)は互いに素、つまり原始ピタゴラス数になるわ」

X「…待てよ、今は存在を証明したいんだから、一つ例を考えたらいいんじゃないか？」

D「m'に数字を入れてみようぜ。m'が偶数だから、まずは2か」

A「すると2m'=4,m'^2-1=3,m'^2+1=5…ってあれ、これさっきのやつだ」

M「m<nという条件を満たさなかったのね。じゃあ、次はm'=4」

D「2m'=8,m'^2-1=15,m'^2+1=17だな。お、これはさっきと違うぜ！」

A「8の2乗は64で、15の2乗は…えーっと」

X「225だな。17の2乗は289で確かにピタゴラスの定理を満たしている」

A「えっ、速い！」

X「20の2乗くらいまでだったら、覚えているからな」

M「このあたりはよく使うからねぇ」

X「ともあれ、(8,15,17)という2つの数の差の最小が2となる原始ピタゴラス数が得られた」

M「m<nという条件を考えると」

    \[(m'^2-1)-2m'>0\]


    \[(m'-1)^2-5>0\]

M「この不等式はm'\ge4を満たす自然数ならすべて成り立つから、2つの数の差の最小が2となる原始ピタゴラス数は無数に存在するわね」

2つの数の差が3となる原始ピタゴラス数

A「おー、なんか面白くなってきた！証明の流れが分かってきたからかな！」

D「せっかくだから次行こうぜ！”2つの数の差の最小が3となる原始ピタゴラス数”か？」

M「さっきと同じ流れでやっていきましょう。m<nとするわ」

    \begin{eqnarray*}m^2+n^2&=&(n+3)^2\\m^2&=&(n+3)^2-n^2=3(2n+3)\end{eqnarray*}

M「さっきまでは展開していたけど、次のように因数分解すると計算が速いわ」

    \[(n+3)^2-n^2=(n+3-n)(n+3+n)=3(2n+3)\]

X「一般に差をaとしても同じだな」

    \[(n+a)^2-n^2=(n+a-n)(n+a+n)=a(2n+a)\]

D「なるほどな。で、今の場合m^2が3の倍数ってことか」

A「ふむふむ。そしたら…mも3の倍数ってこと？」

M「その通りよ。だから、m'を自然数として」

    \[m=3m'\]

M「こう表しましょう。あとはさっきの式に代入して」

    \begin{eqnarray*}(3m')^2&=&3(2n+3)\\9m'^2&=&3(2n+3)\\3m^2&=&2n+3\\2n&=&3m'^2-3=3(m'^2-1)\end{eqnarray*}

M「と、このように式変形できるわね」

A「ありゃ、さっきみたいにきれいにならないね」

D「しかも、最後の式の右辺って3の倍数ってことだよな。ってことは、2nは3の倍数か」

X「付け加えると、2と3は互いに素だから、nが3の倍数になる」

A「待って！mも3の倍数だったから、これって互いに素にならないってこと？」

M「そうなるわね」

D「つまり…どういうことだ？」

M「今2つの数の差が3となるピタゴラス数を考えようとした。
すると、mとnがどちらも3の倍数となり、互いに素でない。
ということは」

X「”2つの数の差の最小が3となる原始ピタゴラス数”は存在しない、ということだな」

D「…」

ディーは何回か計算を見ながら考えていました。

D「今仮定したのは2つの数の差が3だってことと、ピタゴラスの定理を満たすことだけだな。そこから2つの数が互いに素でない、ということが出てきた。
原始ピタゴラス数は3つの数が互いに素であるという条件が必要だが、今の話はそれと矛盾している…ってことか？」

M「アキは理解できたかしら？」

A「ディーの話を聞いて私も分かったと思う！
2つの数の差が3となるピタゴラス数は必ず3の倍数になっている。
だから、原始ピタゴラス数にならないってことだよね？」

X「その通り。もう少し見てみるか…」

n'を自然数としてn=3n'とする。
このとき、6n'=3(m'^2-1)より2n'=m'^2-1
よってm'^2=2n'+1

X「なるほど、m'とn'は2つの数の最小が1となる原始ピタゴラス数になる、ということか」

A「えっ？そうなの！？」

X「まず、n=3n'としたからn+3=3(n'+1)だ。そして、m'とn'は

    \[m'^2=2n'+1\]


という関係を満たしている。これは、差が1となる原始ピタゴラス数の時も出てきた式だ」

A「ホントだ。今日は見たことのある式が出てくることが多いね…」

M「つまり、m=3m',n=3n'で(m',n',n'+1)は原始ピタゴラス数である、言い換えると…
“2つの数の差の最小が3となるピタゴラス数は差が1となる原始ピタゴラス数の3倍のみ”
ということね」

2つの数の差が4となる原始ピタゴラス数

A「原始ピタゴラス数が存在しないってこともあるんだね…。
“2つの数の差の最小が4となる原始ピタゴラス数”だとどうなるんだろ？」

m,nをm<nかつ

    \[m^2+n^2=(n+4)^2\]


を満たす自然数とする。このとき、

    \begin{eqnarray*}m^2=(n+4)^2-n^2=4(2n+4)\end{eqnarray*}

A「だから、m^2は4の倍数で…」

M「2n+4も2で割り切れるから、m^2は8の倍数ね」

A「そっちもあったか！
そしたら…どうしたらいいかな？」

X「mを4の倍数としたほうが計算しやすそうか…」

m'を自然数としてm=4m'とおく。すると

    \begin{eqnarray*}(4m')^2&=&4(2n+4)\\2m'^2&=&n+2\\n&=&2(m'^2-1)\end{eqnarray*}

D「ってことは、nは2の倍数だから…」

A「mが4の倍数ってことは偶数だから…nとmは互いに素にならない！」

M「n=2n'とおくと、n'=m'^2-1で、(2m',m'^2-1,m'^2+1)は差が2となる原始ピタゴラス数ね。つまり…」

X「”2つの数の最小が4となるピタゴラス数はすべて差が2となるピタゴラス数の2倍”ということか」

D「…待て待て。ってことはあれか？差の最小が3となる原始ピタゴラス数も、4となる原始ピタゴラス数も存在しないってことか？」

A「1や2のときには存在していたのにね…」

D「差が5の時も存在しないのか？」

M「やり方は分かってきたから、各自で試してみましょう。アキが5、私が6、数正が7、ディーが8のときで、終わったら、順々に続けてみましょう」

X「そうだな」

A「了解っ！」

D「やってみっか」

ということで、しばらくの間各々で計算してみることにしました。

A「差が5のときは…互いに素にならないなぁ」

M「差が6のときもダメね」

X「差が7の原始ピタゴラス数は…存在しないようだな」

D「おいおい、これ、ずっとないってパターンじゃねぇだろうな…。
…ん、待てよ、これって」

A「次は…差が9のときだね。
でも、本当にずっとないって…」

D「おい、差が8の原始ピタゴラス数が見つかったぞ!!」

A「えっ、ホント！？」

…ということで、予定より長くなったので、ここで一区切りします(^_^;)
書きたいことは出来てきているので、もう少しだけお付き合いください。

この記事を書いたブロガー

sato
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

前の記事

【真理の森の数学セミナー】SS：原始ピタゴラス数のお話

次の記事

【数学小説】真理の森の数学セミナーSS：原始ピタゴラス数③