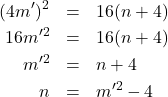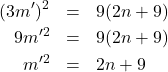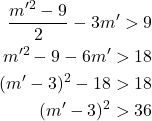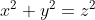【数学小説】真理の森の数学セミナーSS：原始ピタゴラス数③

おはようございます、satoです。

前回に引き続き『原始ピタゴラス数』をテーマに、4人が自由にあれこれする話を書いていきたいと思います。

ところで、前回の話から、途中で気になるところがいくつかある(数学に詳しい人だと特に)かと思いますが、その一部は話が進むと使ったり、修正したりすることもあるので、そのまま見てもらえると嬉しいです。そこもライブ感ということで。

最初から→こちら
前回はこちら

目次非表示

2つの数の差が8となる原始ピタゴラス数
2つの数の差が9となる原始ピタゴラス数
まとめと発展：ペル方程式との関係
あとがき

2つの数の差が8となる原始ピタゴラス数

D「おい、差が $8$ の原始ピタゴラス数が見つかったぞ!!」

A「えっ、ホント！？」

ディーの声を聞いた3人が彼の方に向かいます。

A「どれどれ…」

$m,n$ を $m<n$ かつ
$m^2+n^2=(n+8)^2$

を満たす自然数とする。このとき、
$\begin{eqnarray*}m^2=(n+8)^2-n^2=(n+8-n)(n+8+n)=8(2n+8)=16(n+4)\end{eqnarray*}$

D「このことから $m^2$ は $16$ の倍数になるよな。
さっき、真理がしたみたいに、 $16$ は $4$ の2乗だから、 $m$ を $4$ の倍数とすると…」

$m'$ を自然数として $m=4m'$ とおく。すると
$\begin{eqnarray*}(4m')^2&=&16(n+4)\\16m'^2&=&16(n+4)\\m'^2&=&n+4\\n&=&m'^2-4\end{eqnarray*}$

D「こうなるんだ。あと、さっきやったとき $m<n$ を満たす条件も調べてただろ？それもやってみたぜ」

$m=4m',n=m'^2-4$ かつ $m<n$ より

*** QuickLaTeX cannot compile formula:
\begin{eqnarray*}m'^2-4-4m'&>&0\\(m'-2)^2-4&>&0\\(m'-2)^2&>&4
</blockquote>
D「だから、$m'-2$が$3$以上のときに$m$は$n$より大きくなるんだ。だから、$m'=5$を代入したみたら…」
A「$m=20,n=21$で、$20^2+21^2=841$だね」
D「$841$は$29$の2乗で、3つの最大公約数は$1$だから互いに素、だからこれは原始ピタゴラス数だ！」
X「…確かに、これは今まで出てこなかったやつだな。だが、残念ながらこれは''2つの数の差の最小が$8$''になっていない」
A「ホントだ。最初の2つの差が$1$だ」
D「うわ、マジか…見落としてたぜ」
がっくり落ち込むディー。
M「でも、証明としてはほぼ正解ね。あとは、$m$と$n$の差が$8$より大きい、という条件を確かめればいいわ」
<blockquote>
$n-m>8$より$$m'^2-4-4m'>8$$変形して$$(m'-2)^2>12$$
</blockquote>
M「こうなるから、$m'$は$6$以上ならいいわね。あとは、$(m,n,n+8)$が互いに素である条件を確かめましょう」
<blockquote>
$n$と$n+8$が互いに素になるためには$n$が奇数である必要がある。よって、$n=m'^2-4$より$m'$も奇数である。このとき、$m'-2,m'+2$が奇数かつ$m'$と互いに素であるので、$m=4m'$と$n=m'^2-4=(m'-2)(m'+2)$は互いに素である。以上より、$m'$が奇数ならば$(4m',m'^2-4,m'^2+4)$が互いに素である。
</blockquote>
M「最後は$(m,n,n+8)=(4m',m'^2-4,m'^2+4)$となるから、$(m,n,n+8)$が互いに素ということを示したことになるわね」
D「''$m'$が奇数なら$m'-2,m'+2$と互いに素になる''って本当なのかよ？」
M「そこは、差が$2$のときに示すべきだったわね…。このように証明できるわ」
<blockquote>
$a,b$を自然数として$m'=da,m'+2=db$とおくと、$$2=(m'+2)-m'=d(b-a)$$となるので、$d$は$2$の約数である。さらに$m'$は奇数であることから、$d=1$が成り立つ。よって、$m'$と$m'+2$は互いに素である。
</blockquote>
M「このようにして示せるわね。$m'-2$と$m'$も同様ね」
X「$m'$を$m'-2$に変えればいいだけだな」
D「$n$と$n+1$が互いに素であることを示すのと似ているな」
X「一般に、次のようなことが示せる」
<blockquote>
$m$が$p$の倍数でないとする。このとき、$a,b$を自然数として$m=da,m+p=db$とおくと、$$p=(m'+p)-m'=d(b-a)$$となるので、$d$は$p$の約数である。さらに$m$は$p$の倍数でないから、$d=1$が成り立つ。よって、$m$と$m+p$は互いに素である。
</blockquote>
X「もう少し言うと、$m$が$q$と互いに素な自然数ならば、$m,m+q$は互いに素になる」
D「そこまで示せるんだな…」
X「証明の仕方はさっきのとあまり変わらない」
M「そういうわけで、$m'$が$6$以上の奇数の時に、$(4m',m'^2-4,m'^2+4)$は原始ピタゴラス数になるわね」
D「$m'=7$とすると、$(28,45,53)$だな」
<blockquote>
$$28^2+45^2=784+2025=2809=53^2$$
</blockquote>
D「…確かにピタゴラスの定理も成り立つな。それにしても、この計算大変だぜ！」
<h2 id="i-1">2つの数の差が9となる原始ピタゴラス数</h2>
D「そういや、さっきからアキが何も言ってない気がするが…」
と、ディーがアキのことを探すと、アキはノートに計算をしていました。
D「って、計算してんのかよ！」
A「あ、ごめん…どうしても次が気になって」
と笑いながら返すアキ。
A「あ、でも、チョット待って！もしかしたら差が$9$のときもうまくいくかも！黒板にやってみるね！」
<blockquote>
$m,n$を$m<n$かつ$$m^2+n^2=(n+9)^2$$を満たす自然数とする。このとき、\begin{eqnarray*}m^2=(n+9)^2-n^2=9(2n+9)\end{eqnarray*}

*** Error message:
Unicode character 「 (U+300C)
leading text: D「
Unicode character だ (U+3060)
leading text: D「だ
Unicode character か (U+304B)
leading text: D「だか
Unicode character ら (U+3089)
leading text: D「だから
Unicode character 、 (U+3001)
leading text: D「だから、
Missing } inserted.
leading text: D「だから、$
Unicode character が (U+304C)
leading text: D「だから、$m'-2$が
Unicode character 以 (U+4EE5)
leading text: D「だから、$m'-2$が$3$以
Unicode character 上 (U+4E0A)
leading text: D「だから、$m'-2$が$3$以上
Unicode character の (U+306E)
leading text: D「だから、$m'-2$が$3$以上の
Unicode character と (U+3068)
leading text: D「だから、$m'-2$が$3$以上のと
Unicode character き (U+304D)

A「 $m^2$ は $9$ の倍数で、 $9$ は $3$ の2乗だから…」

$m'$ を自然数として $m=3m'$ とおく。すると
$\begin{eqnarray*}(3m')^2&=&9(2n+9)\\9m'^2&=&9(2n+9)\\m'^2&=&2n+9\end{eqnarray*}$

A「 $m'^2$ は奇数だから、 $m'$ も奇数だね！あとは…」

$m<n$ かつ $n-m>9$ より、
$\begin{eqnarray*}\frac{m'^2-9}{2}-3m'>9\\m'^2-9-6m'>18\\(m'-3)^2-18>18\\(m'-3)^2>36\end{eqnarray*}$

A「 $2$ 乗したら $36$ より大きくなる数だから、 $m'-3$ は7以上！」

$n$ が $9$ と互いに素であるならば、 $n$ と $n+9$ が互いに素である。
よって、 $m'^2=2n+9$ から $m'^2$ 、すなわち $m'$ も $9$ と互いに素である。
$m=3m'$ なので…

A「…ここまではできたけど、この後が難しいかも」

M「どういうところで詰まっているのかしら？」

A「今考えたのは $(m,n,n+9)$ が互いに素になるような $n$ や $m$ の条件だったはずなんだけど、最初の話って逆のように思えて…。何やっているのか混乱しちゃった」

M「少し整理しましょうか。
最初の主張は数正が話していたものよね？」

A「うん、これ便利そうだなって思って使ったの」

M「私たちが考えたいのは『 $(m,n,n+9)$ が互いに素である』ための $n$ や $m$ の条件なのよね？」

A「そうそう」

M「それなら、アキの証明の流れから、次の命題が推測されるわ」

$m'$ が $9$ と互いに素ならば $(3m',\frac{m'^2-9}{2},\frac{m'^2+9}{2})$ は原始ピタゴラス数

M「一方で、この逆も考えられるわね」

$(3m',\frac{m'^2-9}{2},\frac{m'^2+9}{2})$ は原始ピタゴラス数ならば $m'$ は $9$ と互いに素

M「今私達が考えたい問題に対する答えはどちらかしら？」

A「最初のほうかな？」

M「ええ。アキが言ったように今知りたいのは $(m,n,n+9)$ が互いに素になるための $m,n$ の条件。” $m'$ が $9$ と互いに素”がその条件だ、というのが最初の命題の主張なのよ。
“ $m'$ が $9$ と互いに素”が成り立てば、命題から $m=3m',n=\frac{m'^2-9}{2}$ とすれば $(3m',\frac{m'^2-9}{2},\frac{m'^2+9}{2})$ は原始ピタゴラス数となるから」

A「ん～…でも、さっきの差が $8$ のときは、逆をやっているように見えたから…」

M「…確かに、そうね。これだと逆のことをやっているわ。
これは私のミスね」

$n$ が $8$ と互いに素であるとき、 $n$ と $n+8$ は互いに素である。
このとき、 $n=m'^2-4$ なので、 $m'$ も互いに素である。

M「こうするのが正しいわね」

A「ふんふん、じゃあ、 $n$ が奇数になるのは？」

M「 $n$ は $8$ と互いに素だけど、 $8$ の約数は $1$ 以外だと $2$ と $4$ 、 $8$ と $2$ のべき乗しかないのよ。ここで大事なのが、 $2$ で割り切れなければ $4$ でも、 $8$ でも割り切れないってこと」

A「チョット待って、考えてみる！」

そう言って、アキはしばし考えます。

A「…もし $4$ で割り切れたら $4m$ って形になって、 $4$ は $2$ で割り切れるから $4m$ は $2$ でも割り切れる…なんかごちゃごちゃしてきた…」

M「でも、アキが言っていることは正しいわ。
そもそも、 $n$ が $4$ で割り切れるということは、 $n=4\times(\text{整数})$ ということ。整数を $m$ とすると、 $n=2\times(2m)$ とも書けるから、 $2$ でも割り切れる。これは、 $n$ が $2$ で割り切れないという仮定と矛盾するわ」

A「 $8$ で割り切れたときも同じだね」

M「今 $n$ は $8$ と互いに素、ということは $n$ は $8$ の約数では割り切れない。
だから、 $8$ と互いに素な数は $2$ で割り切れない、つまり奇数になるわ」

A「そういうことか！…あれ、それじゃあなんで逆をやったの？
$m'$ と $m'+2$ が互いに素のときにもやっていたけど…」

M「そもそも、私が知りたかったのは $n,n+8$ が互いに素となるような $n$ なのだけど、そのヒントとして、仮に $n,n+8$ が互いに素だと $n$ がどのようになるのかを考えたの」

A「あ、それで最初に $n,n+8$ が互いに素だって考えたんだ！」

M「そこで $n$ が奇数だ、と分かったから、今度は $n$ が奇数なら $n,n+8$ が互いに素かを見てみたのよ。今の場合はちゃんと互いに素になったというわけね」

A「そこがもやもやしてたところかも！
最初にヒントなしだと分からないから、一旦逆を考えた、ってことだよね？」

M「ええ。
ただ、実際には、逆が正しいからと言って元の命題が成り立つとは限らないわ。
あくまで、問題を解くための一つのヒントね」

Aを仮定してBが成り立つからと言って、BならばAが成り立つとは限らない。

A「今は大丈夫なの？」

M「 $m',m'+2$ の場合の方が簡単だからこっちで説明するけど、この場合は” $m'$ の偶奇”と” $m',m'+2$ の公約数”が一対一対応しているのよ」

$m'\text{が奇数}\Leftarrow d=1\Leftarrow m',m'+2\text{は互いに素}$

$m'\text{が偶数}\Leftarrow d=2\Leftarrow m',m'+2\text{の公約数は}2$

M「だから、 $m'$ が奇数であることと $m',m'+2$ が互いに素であることが同値になる」

A「ん～、今のところもう少し説明してほしいかな…」

M「それなら、さっきの証明をもう少し深く見てみましょう」

$a,b$ を自然数として $m'=da,m'+2=db$ とおくと、
$2=(m'+2)-m'=d(b-a)$

となるので、 $d$ は $2$ の約数である。

M「まず、この証明の中で出てきた $d$ は $m',m'+2$ の公約数ね」

A「 $m'$ は $d$ の倍数で、 $m'+2$ も $d$ の倍数だから、 $d$ は2つの数の公約数…うん、大丈夫」

M「そして、 $d$ は $2$ の約数だから、 $d=1$ か $d=2$ のどちらかが成り立つわ。
本当は $d=-1,-2$ もあるけど、 $m'$ が自然数だから、 $d$ は正の数になる」

A「うんうん」

M「今の話から、 $m',m'+2$ の公約数になるのは $1$ か $2$ のどちらかしかないのよ」

A「…」

M「たとえば、 $m',m'+2$ の公約数が $3$ となるとしましょう。
そうすると、 $(m'+2)-m'$ も $3$ の倍数になるはず…よね？」

A「2つの $3$ の倍数の差も $3$ の倍数になる…あれ？
そうしたら $2$ が $3$ の倍数になっちゃう！」

M「そう、矛盾するわ。だから、 $3$ は $m',m'+2$ の公約数にはならない。
同様に $4,5,6,\cdots$ も $m',m'+2$ の公約数にはならないわ。
もしそうなるとしたら、 $2$ が $4,5,6,\cdots$ の倍数になるから」

A「…そっか、 $m',m'+2$ がどちらも $d$ の倍数だとその差も $d$ の倍数になるけど、その差は $2$ だから、 $2$ は $d$ の倍数になる。だから、この $d$ に入るのは $1,2$ のどちらかしかないってことかな？」

と、アキがちょっと不安そうに真理を見ながら話しました。

M「大丈夫、合ってるわよ。
$m'$ がもし奇数、つまり $2$ と互いに素ならば、 $d=2$ とはならないから、 $d=1$ しかない、だから、 $m'$ が奇数なら $m',m'+2$ は互いに素、というわけね」

A「そっか、 $d$ の値によって公約数が対応するから、最初に逆を考えたとき見つけた条件がそのまま使えるんだね。他の場合でもそうなの？」

M「ええ。 $n,n+8$ のときにはこのような対応になるわね」

$n\text{が奇数}\Leftarrow d=1\Leftarrow n,n+8\text{は互いに素}$

$n\text{が偶数}\Leftarrow d\neq1\Leftarrow n,n+8\text{の最大公約数は$2$以上}$

A「うん、真理ちゃんが考えたかったことが分かった気がする！」

M「…できれば、私のことは真理と呼んでほしい…まぁいいわ。
続きを考えましょう」

$n$ が $9$ と互いに素であるならば、 $n$ と $n+9$ が互いに素である。
よって、 $m'^2=2n+9$ から $m'^2$ 、すなわち $m'$ も $9$ と互いに素である。
$m=3m'$ なので、 $ｍ$ と $n$ も互いに素になる。
また、 $m'^2=2n+9$ より $m'^2$ 、すなわち $m'$ は奇数になる。
以上より、 $m'$ が $10$ 以上の $9$ と互いに素な奇数のとき、 $(3m',\frac{m'^2-9}{2},\frac{m'^2+9}{2})$ は原始ピタゴラス数となる。

A「たとえば、 $m'=11$ とすると $(33,56,65)$ で、 $33^2=1089,56^2=3136,65^2=169*5=4225$ だから、ちゃんとピタゴラスの定理が成り立つね！」

まとめと発展：ペル方程式との関係

X「…ふむ、今までの証明を見ていると、こんな予想ができるな」

\begin{itemize}
\item{ $(1)$ } $q$ が奇数の $2$ 乗と $2$ の奇数乗の積のとき、差の最小が $q$ となる原始ピタゴラス数が無数に存在する。
\end{itemize}

D「そうなのか？」

X「ポイントは証明の次の部分だ」

$\begin{eqnarray*}m^2+n^2&=&(n+q)^2\\m^2&=&(n+q)^2-n^2=q(2n+q)\end{eqnarray*}$

X「この後、原始ピタゴラス数が存在した時は $m=\sqrt{q}m'$ とおける場合だった。一方、こうできない場合は $(m,n,n+q)$ は $2$ 以上の公約数を持っていた」

M「ただ、さっきのディーのときみたいに、 $n^2+(n+q)^2=m^2$ という形で存在することもあるから、この場合を考えないといけないわね」

X「それは気になっていた。実際、どうなる？」

M「このまま考えるのは難しそうだから、原始ピタゴラス数の公式を使いましょうか」

A「そんなのあるの？」

M「原始ピタゴラス数は次のようにして得られるわ」

$s,t$ が互いに素、かつ $s<t$ で片方が奇数、もう片方が偶数とする。
このとき、 $(t^2-s^2,2st,t^2+s^2)$ は原始ピタゴラス数になる。

M「ここで、最初の2つの差がどうなるのかを計算すると…」

$(t^2-s^2)-2st=(t-s)^2-2s^2$

M「となるわね。つまり」

$(t-s)^2-2s^2=\pm q$ となる自然数 $s,t$ が存在するとき、 $(t^2-s^2,2st,t^2-s^2)$ は差の最小が $q$ となる原始ピタゴラス数となる可能性がある。

D「なんで $\pm$ がついてるんだ？」

M「さっきの原始ピタゴラス数の表示だと大小関係の条件がないのよ。そして、 $t^2-s^2$ と $2st$ は偶奇が違うから大小を固定することはできない。だから、2つの数の差がどちらでもいいように、 $\pm$ をつけたの」

A「なるほど…」

M「もう一つ、”差の最小が $q$ となる原始ピタゴラス数となる可能性がある”というのは、実際には $q$ より差が小さい2つの数がある可能性もあるから。たとえば、 $q=7$ とすると…」

$t-s=3,s=1$ とすると、 $3^2-2=7$

M「となって、 $t=4,s=1$ は上の方程式を満たすわね。これを $(t^2-s^2,2st,t^2+s^2)$ に代入すると…」

A「 $(15,8,17)$ だね。あれ、これって差が $2$ のときに出てきたやつだ」

M「そう、このような場合があるからあくまで”可能性がある”という表現にしたのよ。ちなみに、 $q=7$ の場合だと $t-s=5,s=4$ も解になっているわ」

$t-s=5,s=4$ とすると、 $5^2-2\cdot4^2=-7$

M「そして、この場合、 $t=9,s=4$ となるけど、これを代入すると…」

D「 $(65,72,97)$ だな」

M「これは確かに差の最小が $7$ となる原始ピタゴラス数ね」

X「ということは、” $q$ が奇数の2乗と $2$ の奇数乗の積以外のとき、差の最小が $q$ となる原始ピタゴラス数は存在しない”というわけではないのか。それにしても、”ペル方程式”と繋がるとは面白いな」

A「ペル方程式？」

X「さっき出てきたこの式のことだ」

$(t-s)^2-2s^2=\pm q$

X「この $q$ を $1$ としたとき、 $x^2-2y^2=1$ をペル方程式という。上の方程式は、ある意味でその拡張と言える」

M「 $x=t-s,y=s$ と置き直すと、 $x^2-2y^2=\pm q$ となるわ」

D「それで、 $q=7$ のときには解が存在するから差の最小が $7$ の原始ピタゴラス数も存在するんだな。たとえば、 $q$ が他の場合のときにはどうなるんだ？」

X「今思いつくのは $q=4$ の場合には、条件を満たす $s,t$ は存在しない、ということだ」

$x^2-2y^2=4$ を満たす自然数 $x,y$ に対して、 $x^2=2y^2+4$ より、 $x^2$ は偶数、つまり $x$ も偶数である。
このとき、 $2y^2=x^2-4$ は $4$ の倍数なので、両辺を $2$ で割ると $y^2$ は偶数である。つまり、 $y$ も偶数である。
以上より、 $x^2-2y^2=4$ の解 $x,y$ はどちらも $2$ の倍数である。
$x=t-s,y=s$ とすると、 $t-s,s$ が $2$ の倍数なので、 $t$ も $2$ の倍数となる。これは $s,t$ が互いに素である、という条件に矛盾する。

A「ということは…差の最小が $4$ となる原始ピタゴラス数は存在しない、ってこと？」

X「そうなる…はずだ。もう少しちゃんと検討したいが。
ただ、正直言うと俺が現時点で分かるのはこのくらいだ。たとえば、 $q=3$ のときに $x^2-2y^2=\pm3$ が自然数の解を持つか…」

といって、上を見上げながら計算をし始めました。

X「 $2y^2=x^2-3$ だから、 $x$ は奇数… $x=3$ だと $9-3=6$ で駄目。
$x=5$ だと $25-3=22$ で駄目。 $x=7$ だと $49-3=46$ で駄目。
$x=9$ なら… $81-3=78$ で駄目…その先も合わないな」

A「す、すごい…暗算してる」

X「…どうも見つからないな。もしかしたら解が存在しないのかもしれないが、こういう方程式の整数解は大きな数になることもあるから、なんとも言えないな」

A「自然数の解が存在しないことってあるの？」

X「たとえば、有名な話だと $x^2+y^2=3$ を満たす整数解は存在しないことが知られている」

M「一方で、 $x^2+y^2=5$ とすると、これは $x=2,y=1$ や $x=1,y=2$ という解が存在するわね。だから、右辺の数字が変わるだけで解が存在しない、ということは十分考えられるわ」

A「数字が変わるだけで、解が存在したりしなかったりするんだ！おもしろ～い！」

M「この辺りは、 $4$ で割った余りが大きく影響しているのよ。その辺りがもっと面白いわよ…」

と言いながら、真理はニヤリと笑っていました。

X「若干スッキリしない言い方になるが、このような予想が立てられる」

\begin{itemize}
\item{ $(2)$ } $x^2-2y^2=\pm q$ の互いに素な自然数解 $(x,y)$ が存在するとき、差の最小が $q$ となる原始ピタゴラス数が存在する。
\end{itemize}

X「もし、上の方程式を満たす互いに素な $x,y$ が存在するとする。
このとき、 $t-s=x,s=y$ とすれば、 $s,t$ も互いに素になる。というところまでは言える。問題は、 $s,t$ の偶奇だが…」

M「 $x,y$ が共に奇数なら $t=x+y$ だから、 $t$ は偶数ね。 $s=y$ は奇数だから、これなら条件を満たすわね。
$x$ が偶数、 $y$ が奇数なら $t$ は奇数。これは条件に合わないわ」

X「 $x$ が奇数、 $y$ が偶数なら $t$ は奇数、 $s$ は偶数となり、これも条件を満たすな。ということは…予想はこうなるか」

\begin{itemize}
\item{ $(2)'$ } $x^2-2y^2=\pm q$ の互いに素な自然数解 $(x,y)$ ( $x$ は奇数)が存在するとき、差の最小が $q$ となる原始ピタゴラス数が存在する。
\end{itemize}

X「この仮定の下なら、互いに素かつ偶奇が異なる $s,t$ を得られるから、そこから2数の差が $q$ となる原始ピタゴラス数が得られる。あとはそれを繰り返すことで、差の最小が $q$ となるものも得られる、としていい…はずだ」

$n^2+(n+q)^2=m^2$ について $m-(n+q)>q$ より $m>n+2q$ となれば、 $(n,n+q,m)$ は差の最小が $q$ となる原始ピタゴラス数である。

X「もし、解が無数に存在するなら、この条件を満たすような $m$ を取ることができるから問題ない。ただ、解が無数に存在するということも実際は確かではない。ペル方程式は解が無数に存在することが知られているが、この拡張したものも同じだろうか…」

M「…思った以上に、深いところに入ったわね」

A「ホントだね～…中学校で習った三平方の定理から、まさかここまで色んなことが見つかるとは思わなかった！」

D「差の最小が $8$ となる原始ピタゴラス数見つけた時はとても面白えって思ったぜ！単なる公式じゃないんだな、これって」

X「整数論の問題は”簡単な”問題でありながら深いところまで考えられるのが面白いところだ。故に、『整数論は数学の女王』と言われたこともある」

M「ガウスの言葉ね」

D「この先はどうなるんだ…？」

M「そこが気になるなんて…ディーもだいぶ数学に興味を持ってきたわね」

D「まぁ、ここで色々やったらな…」

X「この先は本当に数学の専門の分野になる。単数とかその辺りだったか…」

M「次は是非、そこまで行きたいわね」

D「できれば、具体的な例をたくさん出してくれると助かるぜ」

あとがき

というわけで、以上で『原始ピタゴラス数』に纏わる森の冒険は終わりになります。
最初にも書きましたように、最初は『日曜数学 Advent Calendar 2020』の第十三日目の記事としてこちらを書く予定でした。
実際には、その日にはフェルマーの最終定理の説明とかで終わってしまい、その次で問題篇、年をまたいで続編となりました。

この物語は、数学が専門でない(興味はあるけど、得意でない/苦手)な人(ディーやアキみたいな)に向けて、専門の人(真理や数正みたいな)がしている数学を説明するところが大事です。その過程で数学をやっている人がどのように考えていて、どのように問題を解くのか、が色々見つかったり、時に深い問題に出会う、そんな物語です。

今回の場合、当初考えていたのは $(m,n,n+q)$ の形の原始ピタゴラス数で、このときどうなるかは、最後の数正の予想 $(1)$ で挙げました。
ところが、書いている途中で $(n,n+q,m)$ の形の原始ピタゴラス数については全く考えていなかったことに気づき、ディーが差が $8$ のとき、途中でミスをしたことをきっかけにして、最後に考えてみたら、なんとペル方程式(の変化版)と繋がった、という想定外のことが起きました。

ちなみに、最後の $x^2-2y^2=\pm3$ が自然数解を持つかどうか、ですが、これは次のようにして分かります。

この方程式を $\mod\ 3$ の世界、つまり『 $3$ で割った余り』に着目して考える。すると、
$x^2-2y^2\equiv 0\ (\mod\ 3)$

となる。さらに $-2\equiv 1\ (\mod\ 3)$ なので、
$x^2+y^2\equiv0$

となる。ところで、任意の自然数 $x$ に対して $x^2$ を $3$ で割った余りは $0$ か $1$ にしかならないので、
$x^2+y^2\equiv0\Rightarrow x\equiv y\equiv 0$

である。以上より、 $x^2-2y^2=\pm3$ が自然数解を持つとすると、 $x,y$ はどちらも $3$ の倍数である。これは $x,y$ が互いに素であることに矛盾する。
以上より $x^2-2y^2=\pm3$ の互いに素である自然数解は存在しない。