宇宙際タイヒミュラー理論入門を読んでみた。その3 | 摂理研究所/キリスト教福音宣教会

おはようございます、satoです。

不定期更新、京大数理研望月新一教授が作り出した新理論「宇宙際タイヒミュラー理論」を解説した星裕一郎講師による論文「宇宙際タイヒミュラー理論入門」を読んで、自分が分かる範囲で解説していくシリーズ第四弾です。
…なかなか続けて更新できていませんでしたが、望月新一教授の4連論文がついに専門誌に掲載されることが決まったこともあり、続けて自分が読める範囲で解説…というよりは私が感じたことを書いていこうと思います。

目次非表示

前回までのあらすじ
逆極限を図で説明してみた
もう少し具体的に…
どうして、こんなややこしいことをしているのか

前回までのあらすじ

長らく書いていなかったので、これまでのあらすじを書いていこうと思います。

星裕一郎さんの論文の最初に「円分物」と呼ばれるものが出てきます。これはTate捻り $\widehat{\mathbb{Z}}(1)$ と呼ばれるものである、と論文には書かれています。いくつかの定義が書いてあったのですが、その一つがこちらでした。

(標数 $0$ の) 代数閉体 $\Omega$ に対する $\Lambda(\Omega) \overset{\text{def}}{=} \lim_{\leftarrow n}\mu_n(\Omega)$
—　ここで, $n \ge 1$ に対して, $\mu_n(\Omega) \subset\Omega$ は, $\Omega$ の中の $1$ の $n$ 乗根のなす群.

$\zeta_n\in\mu_n(\Omega)$ とすると、 $\zeta_n$ は $\Omega$ の中の $1$ の $n$ 乗根で、 $\zeta_n^n=1$ が成り立ちます。
とりあえず代数閉体 $\Omega$ を複素数体 $\mathbb{C}$ とすると、 $\mu_n(\Omega)$ は「半径が1の円に内接する正n角形の頂点(でそのうちの一つが $(1,0)$ にあるもの)」という事ができます。
前回は、 $\lim_{\leftarrow n}$ という記号が逆極限と呼ばれる操作であって、それは $(\zeta_2,\zeta_3,\zeta_4,\ldots)$ と $\mu_n(\Omega)$ の元を並べることになる、ということを書きました。しかし、改めて読むとこれが何を意味するのかよくわからないな…(´・ω:;.:…と思いました。
そこで、今日はこれを図で見ながらもう少し詳しく説明していきたいと思います。

逆極限を図で説明してみた

$n$ が2以上の自然数だとうまく説明するのが難しいので、ここでは $n=3,9,27,81,\ldots$ というように「3のべき乗」で表される数とします。
そうすると、 $\mu_n(\Omega)$ は次の図の赤点になります。

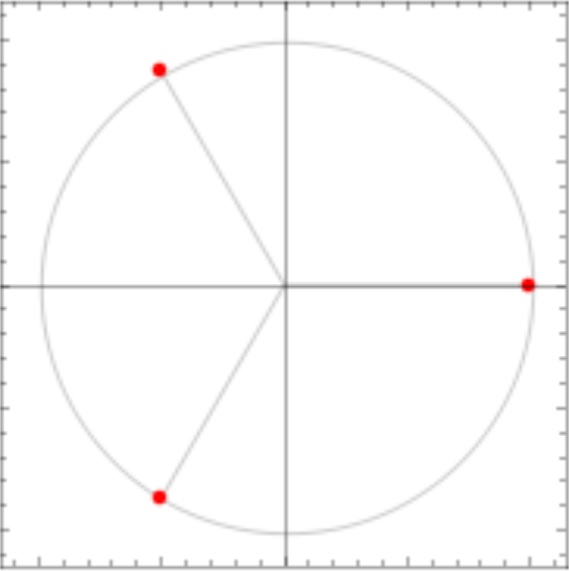
n=3のとき

n=9のとき

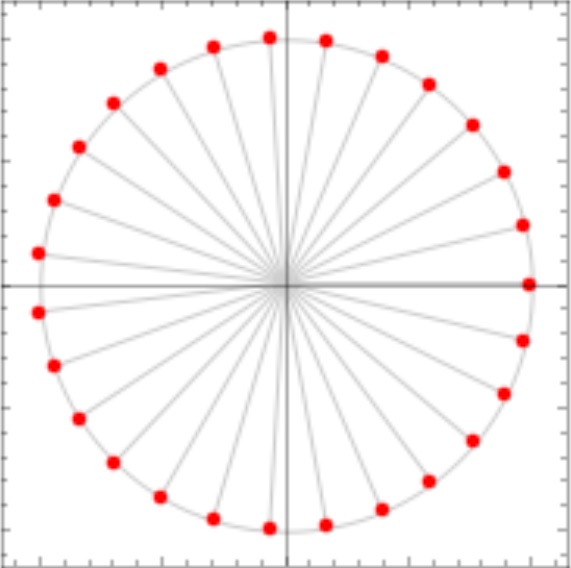
n=27のとき

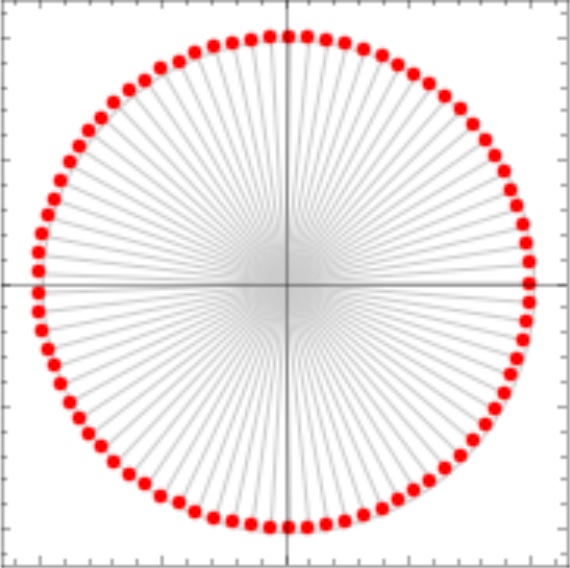
n=81のとき

指数が大きくなるほど、 $\mu_n(\Omega)$ は円形に近づきます。
言い換えると、円周上にある各頂点の間が狭くなっています。そこで、次のようなことが考えられます。
指数を大きくしていくことで、ある円周上の点に限りなく近づく「頂点の集まり」を作れるのでないか？
このような点があることは容易に想像できます。そこで、このような点の集まりを $\lim_{\leftarrow n}\mu_{3^n}(\Omega)$ と置くことにします。これが逆極限です。

もう少し具体的に…

円周上の点は「 $|z|=1$ を満たす複素数全体」として表すことが出来ます。極座標を使うと

$\{e^{2\pi i\theta}|0\le\theta<1\}$

と表せます。なので、今の話は

$0\le\theta<1$ の実数で「3のべき乗を分母とする分数」によって限りなく近似できるもの

を集めることと同じです。
例えば $\theta=\frac{1}{2}$ とすると、

$\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\cdots+\frac{1}{3^n}+\cdots=\frac{1}{3}\sum_{n=0}^\infty\frac{1}{3^n}=\frac{1}{3}\frac{1}{1-\frac{1}{3}}=\frac{1}{2}$

となりますので、「 $\frac{1}{2}$ は $\frac{1}{3^n}$ たちによって近似される」ということが分かります。

実際には、 $\lim_{\leftarrow n}\mu_{n}(\Omega)$ は2以上の自然数全体を動きますので、
$\theta=\frac{q}{r}$ なら、 $e^{i\theta\pi}$ は $\mu_{r}(\Omega)$ の元、つまり $\lim_{\leftarrow n}\mu_{n}(\Omega)$ の元になります。
そこで、実際に問題になるのは0と1の間にある無理数のときです。
私個人としては、円周上の全ての点が $\lim_{\leftarrow n}\mu_{n}(\Omega)$ の元になるというのはちょっと怪しい気もしますが…。

どうして、こんなややこしいことをしているのか

さて、ここまで読んでいただいて「やけにややこしいことをしている」と感じた人は多いと思います。
(私の説明の下手なところも多分にあると思います、そこはご容赦ください…)
そもそも、 $\Omega=\mathbb{C}$ の時は、円周上の点はさっきも書いたように $e^{2\pi i\theta}$ と表せます。それを、こんな逆極限という複雑な操作をして表現しようとしているのはどうしてでしょうか？

簡単に言うと、この表記が真価を発揮するのは $\Omega$ が他の代数閉体の時です。
例えば、 $\Omega$ として考えられるのは、代数的数全体(つまり、有理数係数のn次方程式の解となる数全体) $\overline{\mathbb{Q}}$ や $p$ 進数体 $\mathbb{Q}_p$ の代数閉包等です。
これらは $\mathbb{C}$ と違ってバラバラ(離散的)になっていますので、円を「描く」ことが出来ません。
また、例えば $\mathbb{Q}_p$ で $|z|_p=1$ を満たす数というと $p$ で割り切れない( $p$ ベキの倍数で表せない)数全体なので、これが円というのはなんとなく違う感じがします。

実は、数論幾何学や代数幾何学において「円周」というのはとても重要な図形です。 $\mathbb{C}$ の場合はそれがきれいな円で表せたのですが、それ以外の代数閉体でも表現できないか？というのが「円分物」の存在理由かと私は思います。
実際、 $\lim_{\leftarrow n}\mu_{n}(\Omega)$ なら、似たような性質が成り立つことが示せるのではないか…と思っています。詳しくは分かりませんが…。

以上、ここまでが円分物についてでした。
他にも円分物の定義がありますが、(特に2番目のものは)私の知識の足りなさもあって説明できません…。
しかし、ここからが宇宙際タイヒミュラー理論の重要なところになりますので、ここで一旦円分物の話を終えたいと思います。