【数学小説】真理の森の数学セミナー～積分編③～ | 摂理研究所/キリスト教福音宣教会

<1/31編集スマホに合わせて一部数式のサイズを変更しました。何故か数式の最後に番号が付いていますが、これについては現在解決策を検索中です…。>

「…気持ち悪いわね」

「えっ？」

真理の一言に反応する3人。

「…この証明、確かに公式が成り立つことは分かるのだけど”どうして”成り立つのかは教えてくれてないわ。
複雑な計算をするのはいいけど…」

真理は式を指差しながら、一つ一つ言葉を重ねました。

「どうして $\frac{1}{6}$ が出て来るの？どうして $(\beta-\alpha)^3$ なの？
確かに $x^2$ の不定積分は3乗になるから3乗はそれほど不自然でないけど、 $\beta^3-\alpha^3$ でないのはどうして？」

その言葉を黙って聞く三人。

真理は「式の本質」を見る心を持っています。
より正確には「式の背景にある数学の世界」を知ることを常に求めています。
それが「どうして」という質問に繋がるのです。

「全ての式変形には発想の根源となるものがある」

それこそ、真理の考える「数学の森」なのです。
そして、この質問に答えることこそが、このセミナーの方針でもある「数学の森を散策する」ことなのです。

「” $\frac{1}{6}$ ”…どこかで見たことがある気がするのよね…」

そう話しながら、真理は一人思考の森に入り込みました。

「…それにしても…」

アキは二人が書いた証明を改めて見ながらつぶやきました。

「これって、ホントにややこしいね…。
私だったら、一人で計算できないなぁ」

「全くだ。俺ももう一回計算しても間違う気がするわ…」

そのつぶやきにディーも同意します。
そこに数正が答えました。

「実は…もっと簡単に求めることが出来る」

「え、そうなの！？」

「マジかよ！そしたら、俺の計算は一体…」

「ただ、この計算はある計算法が必要で、これを説明するのは少し大変なんだ。
だから、あえて愚直に展開する方法で証明した」

「…うーん、そうなんだ…。
でも、せっかくだからその証明も知りたいな」

アキはその証明に興味を示していました。

「分かった。
そうしたら、少し丁寧に説明していこう。
ディーは一度見たことがあるはずだ。その計算法の名前は…

“部分積分法”

という」

「ぶ、部分積分法…なんだか難しそう…」

その名前に少し引き気味のアキ。

「まぁ、名前こそ難しいように感じるし、使うのにちょっとコツがいるがとても便利な計算法だ」

そう言いながら、数正は黒板に次の数式を書きました。

${\footnotesize \int_{\alpha}^\beta f'(x)g(x)dx=\left[f(x)g(x)\right]_{\alpha}^\beta-\int_{\alpha}^\beta f(x)g'(x)dx}$

「う、うぅぅ…」

式を見て困惑するアキ。そんな彼女に数正は不安を解くように語りかけました。

「式だけを見てしまうと複雑だと思う。
これから一つ一つ意味を説明するから、一緒に見てみよう」

「うん…」

「まず、左辺は2つの関数 $f'(x)$ と $g(x)$ の積 $f'(x)g(x)$ を $\alpha$ から $\beta$ までで積分したものだ。
この部分積分法は”2つの関数の積に対する積分”の計算方法だ」

「…” $f'(x)$ ”なの？” $f(x)$ ”でなくて？」

「そこについてはもう少しあとで説明しよう。
ひとまず左辺については大丈夫か？」

「うん、ひとまずは…とりあえず”2つの関数があって、その掛け算を積分した”ということなんだよね？」

「その理解で合っている」

「…ん～～」

二人の側で聞いていたディーが唸っていました。

「具体的な例で説明してくれ…」

「そうだな。
たとえば、 $y=x$ と $y=e^x$ という2つの関数があったとしよう」

そう話しながら、数正は黒板に2つの関数を書きました。

「この関数を掛け算するとどうなる？」

「… $y=xe^x$ だよな？」

「そうだ。その関数を積分する」

$\int xe^xdx$

「…この関数の積分ってどうなるんだ？」

「直接”微分したら $xe^x$ になる”ような関数というのを見つけるのは難しい。
部分積分法は、こういうものを求めるためにある」

「なるほどな…」

ディーも納得したところで、数正は話を進めました。

「では、右辺を見てみよう。
右辺は2つの式の差になっている。 $\left[f(x)g(x)\right]_{\alpha}^\beta$ と $\int_{\alpha}^\beta f(x)g'(x)dx$ だ」

「…確か、 $\left[\right]_{\alpha}^\beta$ はカッコの中に $\beta$ を代入したものから $\alpha$ を代入したものを引くんだよね？」

「そうだ。この場合は $f(x)g(x)$ に $\beta$ を代入した値と $\alpha$ を代入した値の差になる。つまり、こうだ」

$\left[f(x)g(x)\right]_{\alpha}^\beta=f(\beta)g(\beta)-f(\alpha)g(\alpha)$

「あれ？」

黒板に数正が書いた数式を見ながら、アキはあることに気づきます。

「 $f(x)g(x)$ になってる！さっきは $f'(x)g(x)$ だったのに…」

「そこだ。この部分積分法の重要なところは”掛け算の片方を積分する”というところにある。
さっき” $f(x)$ ”でなく” $f'(x)$ ”にしたのは、この話をしたかったからだ。」

「ここは積分でなくて、代入してってなるんだな」

「ああ、この式はより正確には

$\int_{\alpha}^\beta(f(x)g(x))'dx$

になる。つまり、 $f(x)$ と $g(x)$ の積の微分だ。
$f(x)$ の積分というのは”微分して $f(x)$ になる関数”を求めることだから、最初に書いた式になる、ということだ」

「2つの関数の積の微分の積分…なんかややこしいな」

「微分より導関数という言葉を使うと良い。
2つの関数の積の導関数の定積分、それが右辺の最初の式の意味だ」

「うーん…」

数正の説明を聞いてもまだ納得が出来ていないアキ。

「今までの流れを振り返ろう。
俺達は $f'(x)$ と $g(x)$ という2つの関数の積の積分を考えたい。
その時に、まず $f'(x)$ の積分である $f(x)$ と $g(x)$ の積の $\beta$ での値と $\alpha$ での値の差を計算した。
大事なのは、2つの関数の内片方を積分…ややこしいな。片方の原始関数ともう片方の積を考えたということだ」

「原始関数ってなんだっけ？」

「今は”微分して $f'(x)$ になる関数”と考えていい」

「あ、 $f(x)$ のことなんだね。ちょっと分かってきた！
つまり、最初は片方を積分してから掛け算したものを考えるんだね！」

「そういうこと。そろそろ次の式を見てみよう」

$\int_{\alpha}^\beta f(x)g'(x)dx$

「こっちは積分のまんまなんだね」

「ああ。さっきは $(f(x)g(x))'$ の積分をしたから、 $[]$ に変わっていたのに対して、こっちは $f(x)g'(x)$ を積分している。
これは微分された関数でないから、積分の形のままなんだ」

数正の言葉を聞きながら黒板の数式をじっと見ていたアキはあることに気づきました。

「…あれ？今度は $g'(x)$ になってる。さっきは $f'(x)$ が $f(x)$ に変わったけど、今度は $f(x)$ はそのままで $g(x)$ が微分されているね」

「そこだ！」

そのアキの気づきに数正は思わず熱く反応しました。
数正は数学好きなので、良い気付きがあると熱くなるのです。

「この2つ目の式で最も大事なのは” $g(x)$ を微分した”ということだ。
つまり、こっちでは先程積分しなかった関数を微分してから、2つの関数 $f(x)$ と $g'(x)$ の積の $\alpha$ から $\beta$ までの積分を考えた」

「…” $f(x)$ ”ってことは、最初に積分したものはそのままなんだな」

ディーも数式を眺めながら気づいたことを口にしました。

「良いところに気づいた。そこも大事だ。
この公式の計算の順番をまとめるとこうなる」

$f'(x)$ を積分する(原始関数 $f(x)$ を求める)
↓
$f(\beta)g(\beta)-f(\alpha)g(\alpha)$ を計算する
↓
$g(x)$ を微分する( $g'(x)$ を求める)
↓
$f(x)g'(x)$ の $\alpha$ から $\beta$ までの積分を考える

「そして、最後に2つの値の差を引く。
つまり、2つの関数 $f(x)$ と $g(x)$ の積 $f(x)g(x)$ の積分を考える時に、直接考える代わりに” $f(x)$ の原始関数”と $g(x)$ の積の値の差、” $f(x)$ の原始関数”と $g'(x)$ の積の積分を計算する、というのが部分積分法だ。
この動きを図でまとめるとこうなる」

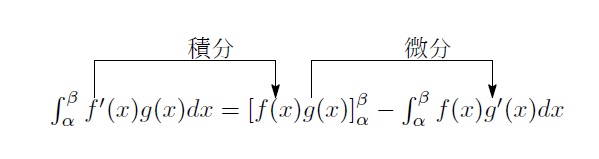
「なるほどー！最初の関数を積分して、その次にもう一つを微分して積分の計算をしていくんだね！」

アキは部分積分法のやり方について理解できたのか、歓声をあげていました。

「…やっぱり実際に計算するのを見たいわ。
前よりは理解できた気はするが、使えるかどうか…」

一方、ディーも少し消化できたようですが、まだちょっと突っかかるところがあるようです。

「そうだな、そもそもこの話をしたのは” $\frac{1}{6}$ 公式”を証明するために部分積分法を使うと簡単になる、という話だった。
だから、部分積分法で証明してみよう」

「…あ、積分の中が $(x-\alpha)(x-\beta)$ って掛け算の形だから使えるんだ！」

「そうだ。では、実際に計算してみよう。まず、 $(x-\alpha)$ を積分すると…」

「確か $\frac{1}{2}(x-\alpha)^2$ だったか？」

「ああ。これと $(x-\beta)$ の掛け算をして…」

「その後、残った $(x-\beta)$ を微分するんだよね！」

「そして、最初の $\beta$ を代入した値と $\alpha$ を代入した値を…」

「その必要はない」

「えっ？どうして？」

「 $[]$ の形を見ると $(x-\alpha)^2(x-\beta)$ となっている。
これは $\alpha$ と $\beta$ のどちらを代入しても0になる」

「…あ、ホントだ！」

「この計算のミソはこれにある」

「さっきの数正の計算でもあったよな、 $(x-\alpha)(x-\beta)$ を残してってやつ」

「そうだな、”式の形を見て工夫する”ということだ」

「じゃあ、最初の式は0になるね。これは簡単だ！」

「次の式は $(x-\beta)'=1$ だから…」

$\begin{eqnarray*}{\footnotesize&&\int_\alpha^\beta(x-\alpha)(x-\beta)dx\\&=&\left[\frac{1}{2}(x-\alpha)^2(x-\beta)\right]_\alpha^\beta-\int_\alpha^\beta\frac{1}{2}(x-\alpha)^2(x-\beta)'dx\\&=&0-\int_\alpha^\beta\frac{1}{2}(x-\alpha)^2dx\\&=&-\frac{1}{2}\left[\frac{1}{3}(x-\alpha)^3\right]_\alpha^\beta\\&=&-\frac{1}{6}(\beta-\alpha)^3}\end{eqnarray*}$