→積分編⑦
「区分求積法…」
その名前を聞いた二人しばし沈黙していました。
「”区間を細かく分けて面積を求める方法”だから、区分求積法」
「言われてみれば…分からなくもないな」
真理の説明で腑に落ちるディー。
「名前だけ聞くと難しそうだけど…これって今まで話していたことをまとめたの？」
「ええ」
そういって、真理は黒板に書いた式をしばし注視していました。
「…積分する区間をちゃんと決めたほうが良いわね。区間の始めを
、区間の終わりを
と置いて、今までの話をもう一度振り返りましょう」
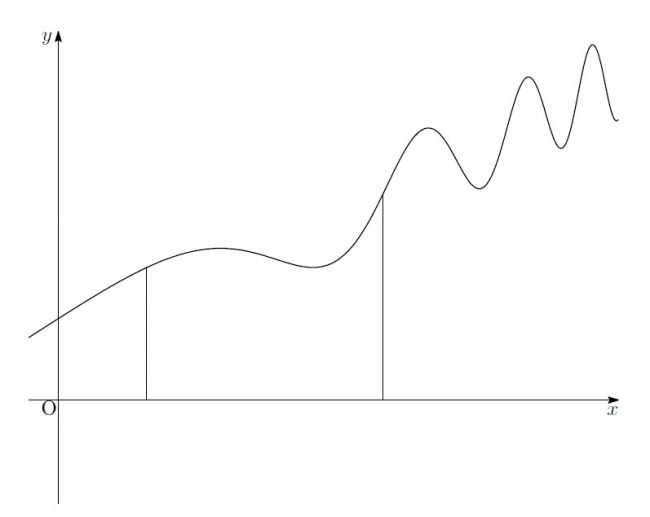
「このような図形があったとすると…」
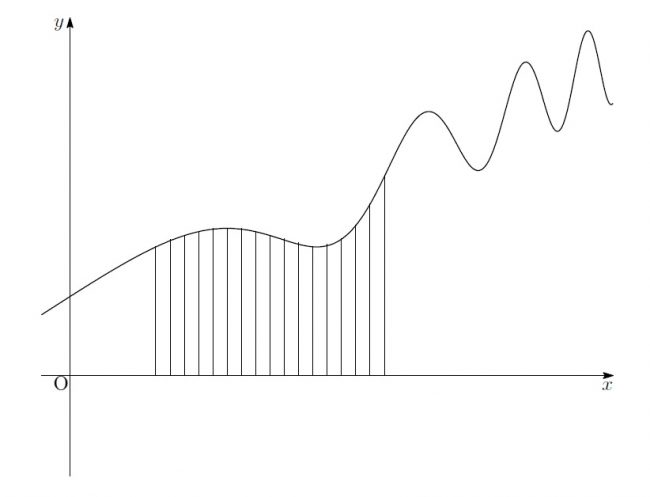
「まず、2つの直線の間を細かく分ける。ここではn等分したとしましょう」
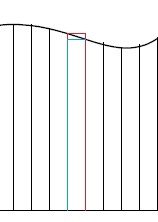
「次に、細かく分けた区間の中でこのように”高さが最大になるところ”と”高さが最小になるところ”を見つけて、赤と青の長方形を作る」
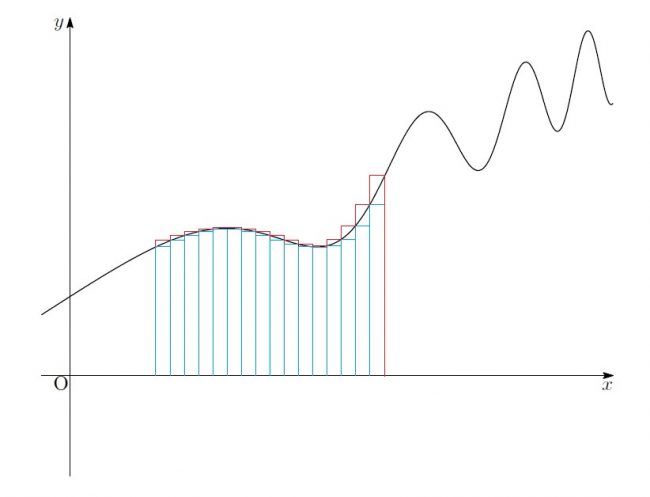
「すると、グラフは赤い図形と青い図形の間に挟まれる形になるわ。つまり、グラフの面積は赤い図形の面積と青い図形の面積の間になるわけね」
「それで、もっと細かく切るほど赤と青、2つの図形の面積の差が縮まって、グラフの図形の面積と一致する…うーむ…」
ディーがその言葉をつぶやきながら唸っていました。
「…本当にそうなるのかよ？
やっぱり具体的な例がないと信じられんわ…」
「それは…グラフの面積と一致するってことかしら？それとも…」
「両方だな…なんとなくはそうなりそうだけど、赤い図形の面積と青い図形の面積が一致するのも怪しいし…」
「それは、いい感覚ね」
「へっ？」
「”赤い図形の面積と青い図形の面積が一致する”かどうかはどの関数のグラフかによるわ。
このことが成り立つとき、”関数
はリーマン積分可能”というのよ」
「…リーマン積分？」
「リーマンってなんか聞いたことある気がする！」
「数学者のベルンハルト・リーマンが定義したから”リーマン積分”なのよ。
ちなみに、彼はゼータ関数についての未解決問題”リーマン予想”を出した人でもあるわ。その辺りで聞いたことがあるのかしら…」
「…リーマン予想は聞いたことないけど、なんかお父さんがアメリカの金融会社が何たら…って話のときにリーマンって名前を出してた気が…」
「なんのことかしらね？」
アキが話してるのはおそらく”リーマンショック”で出てきたリーマン・ブラザーズのことです。もちろん、これは数学者のリーマンとは関係ありません。
ちなみに、数学者の方はRiemann、金融会社の方はLehmanなので、綴りも違います。
「それはそうと…ここでは赤い図形の面積と青い図形の面積、それぞれの極限がが一致するとしましょう。そのとき、この極限がグラフの面積と一致することは次のように説明できるわ」
「青い長方形は各区間の”最小値”が高さである長方形よ。よって、これを足し合わせた面積はグラフより小さい」
![\[L_n\le S \ ({}^\forall n\in \mathbb{N})\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-f0513fa151aa37f85caf84fd8274b037_l3.png "Rendered by QuickLaTeX.com")
「まぁ、それはそうだな…」
「よって、この極限…言い換えると”限りなく細かく分割した図形の面積”はグラフの面積以下になる、というのはなんとなく分かるかしら？」
![\[\lim_{n\rightarrow\infty}L_n\le S\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-571cbdb6316565935d6bfac44095d14f_l3.png "Rendered by QuickLaTeX.com")
「…極限って、この場合”
を限りなく大きくしたときの
が近づく値”ってことだったっけ？」
「ええ、それで大丈夫よ」
「だったら、私は大丈夫！」
「…まぁ、ここまでは納得できるぜ」
「それなら、あとは赤い方ね。赤い長方形は各区間の”最大値”が高さよ。
ということは、この図形を足し合わせた図形の面積はグラフの面積より大きくなる」
![\[S\le M_n \ ({}^\forall n\in \mathbb{N})\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-0539003f8f4cc03844e37d8f63207da9_l3.png "Rendered by QuickLaTeX.com")
「…あ、ってことは”赤い図形の面積の極限”はグラフの面積以上になるのか！」
![\[S\le\lim_{n\rightarrow\infty}M_n\]](https://setsuri-nihon.net/wp-content/ql-cache/quicklatex.com-52156815433ba96c27589e5a0e2e6235_l3.png "Rendered by QuickLaTeX.com")
「そういうこと。そして今この2つの極限が一致するとしたら、この極限は”グラフの面積以下”かつ”グラフの面積以上”になる。
それを満たすような数というのは…」
「…自分自身、つまり”グラフの面積”そのものしかない、ってことか！」
ディーは興奮した様子で矢継ぎ早に話しました。
「だから、この極限はグラフの面積になるってことなのよ」
「なるほどなぁ…ちょっと極限が出てきて大変かな～って思っていたけど、一つ一つ振り返ると、なんとなくだけど…掴めてきた感じはする！」
真理の話を聞いて、アキはスッキリした様子で話しました。
「実際に使えるようになるくらいに理解するにはもっと色々な例を計算するといいのだけど…今日は”
公式”に集中しましょう」
「そうだな、じゃあ早速…」
「まずは
ぐらいで実際に分割してみましょう」
「…って、えっ！？計算しないのかよ？」
真理の提案に驚くディー。それに対して冷静に答えました。
「”具体的な話”が良いのでしょう？焦らずに、具体例で考えましょう。
そうすると、単なる計算よりもっと良いことが分かるかもしれないわよ」
→積分編⑨
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
私と発達障害2024年4月18日心が不調になった時の整え方
日々感じること2024年4月17日自分の理解の甘さを痛感した話
聖書＆御言葉2024年4月16日次元を上げたい、というところまで行かない私へ。
日常生活2024年4月15日私が今日生きられることへの感謝。
