おはようございます、satoです。
最近見た論文で面白いなと思ったものを紹介します。
これはGrothendieckが提唱した「遠アーベル幾何学」がどのように発展していったのかについて歴史を追って書いてある論説です。
Grothendieckは「基本群によって決定される図形が存在する」という哲学のもと、双曲代数曲線の時には予想を立てていました。
しかし、実際のところ「どのような数学になるのか」まで彼は話していませんでした。
この論説にも書いていますが、そもそも彼がこの哲学を思いついたのは「Belyiの定理」、射影直線上3点で分岐する被覆によって全ての「代数的数体」上の非特異完備代数曲線が表されるという事実からです。
これだけでもとても面白いのですが(全ての曲線が3点分岐の情報だけで分かるだなんて…)、さらにこれがあるグラフの情報から決まるということが知られています。
このグラフが「子供のデッサン」というのですが、見た目は本当に子供のデッサンみたいなのです。
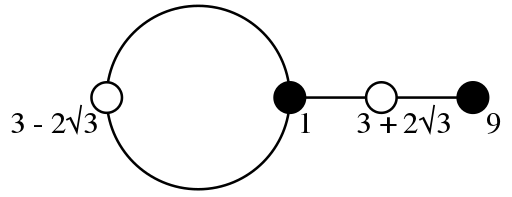
たとえば、これは 
から得られるグラフなのです。詳しい意味は私もよく分かっていません(´・ω:;.:…
ただ、こんなに単純なグラフから曲線の情報を得られる、というのはとても面白いです。
こういう事実から始めて「遠アーベル幾何学」を打ち立てたのはとても画期的なのですが、それは「離散的」な群から幾何を再現しようという話だからです。
ちなみに、今望月新一教授がしようとしているのもこの「群から幾何を復元する」ということのようです。
さらに、Grothendieckは「ガロア-タイヒミュラーの積み木遊び」なんてものも考えたらしいです。
子供のデッサンといい、子供っぽい遊びになぞらえて理論を形成していっているのですが、もしかしたらこれは彼が自伝で話していた「自分の中にある子供の声に忠実になる」ってことなのでしょうか？
しかし、数学は特に社会や実益とは無縁の「趣味の世界」になることが多いです。
それ故「子供のような心で」数学をするのがとても大事です。「これをやっていて何が得られるのか」なんて考えていたら、数学はやっていられません(笑)
ある意味、信仰の世界と同じなのかもしれませんね。
そのとき、イエスに手をおいて祈っていただくために、人々が幼な子らをみもとに連れてきた。ところが、弟子たちは彼らをたしなめた。するとイエスは言われた、「幼な子らをそのままにしておきなさい。わたしのところに来るのをとめてはならない。天国はこのような者の国である」。-マタイによる福音書19章13-14節
信仰の世界も、「祈ったらお金が得られるのか」とか「聖書を読んで飯が食えるか」とか色々考えていたらうまく行きません。
そういうことを考えていたイスラエル民族はモーセがカナンに導いていた時に不平不満を漏らし、結局カナンの地に行けませんでした。
このことを考えると、信仰も数学も「ひとまず現実は置いといて子供のように没頭する」のが一番早い道なのかなと思います。
私ももっと子供のように素直で純粋な気持ちで信仰も数学も取り組みたいと思います。
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
日々感じること2024年11月13日運動不足？
日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
