おはようございます、satoです。
先週話したとおり、数学小説『真理の森の数学セミナー』の公開を再開したいと思います。
今回は前に書いていた『積分編⑨』の話をしたいと思います。
(前回の展開でかなり流れが長くなってしまって、どうするか迷っていたのが止まった原因です…)
だいぶ前の話なので、これまでの話をリンクで貼っておきたいと思います。
そう話して、真理は黒板に数式や図を書き込みました。
「今放物線の式は![]() としましょう。これが一番わかりやすそうだから」
としましょう。これが一番わかりやすそうだから」
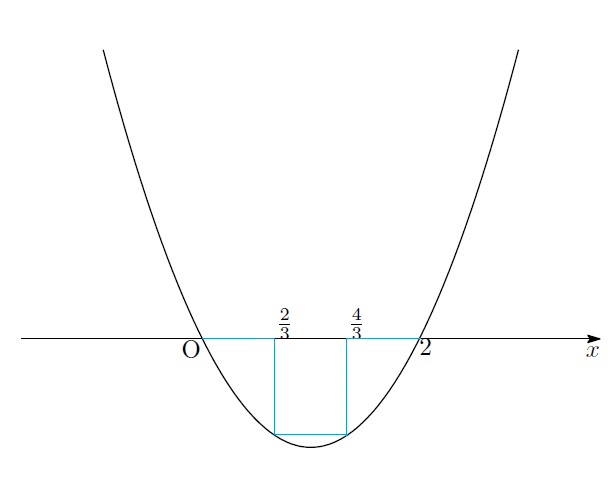
「まずは![]() のとき、つまり区間を三等分したときを考えましょう。このとき、一つの区間の長さは?」
のとき、つまり区間を三等分したときを考えましょう。このとき、一つの区間の長さは?」
「直線の長さは2だから…三等分すれば![]() か?」
か?」
「そうよ。だから、![]() のとき
のとき![]() は次のようになるわ」
は次のようになるわ」
「一つ注意しておくわね。
さっきまでは”グラフが![]() 軸より上”にあったから、青い長方形は”最小値”を高さ、赤い長方形は”最大値”を高さとしていたわ。
軸より上”にあったから、青い長方形は”最小値”を高さ、赤い長方形は”最大値”を高さとしていたわ。
だけど、今は”グラフが![]() 軸より下”のところを考えているわ。
軸より下”のところを考えているわ。
ここでは、さっきの話と合わせるため”青い図形はグラフの内側、赤い図形はグラフの外側”にあると考えましょう」
「えーっと…ということは…」
「つまり、”青い図形は最大値、赤い図形は最小値が高さ”ということにするというわけね。
負の値を考えるから大小が逆になるけど、辺の長さで考えると同じことを話しているわ」
「そういうことか…。言われてみればまぁ自然だが…なんでまたこんな回りくどい説明を?」
「…”厳密に”しないと気が済まないから人もいるよ。
“最大値、最小値が逆だ”って言われる前に、ね」
「…なんだか、引っかかる言い方だな。
数学をする上では厳密さは必要だ」
真理の言葉に若干不服そうに返事する数正です。
「それはそうよ。ただ、今みたいに”考えを説明する”ときには多少厳密さを犠牲にしたほうが分かりやすいこともあるでしょう?」
「まぁ、それはそうだ…だが」
「…この話をすると長くなりそうだから、続けましょうか」
「…まぁ、いい」
まだ言いたいことがありそうな数正ですが、一旦議論を進めることにしました。
「さて、改めて青い図形を見ましょう。
グラフの内側にあるから、”図形の面積”としては”グラフの面積より小さい”わ」
「最初のところは0なんだね。
だったら、青い図形の面積は簡単そう!」
「簡単そう…ってか、実際に計算するのはひとつだけだよな」
「そうね。実際に計算してみましょう。![]() のときは…」
のときは…」
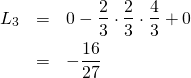
「こうなるわね」
「端っこの2つが0になるのは良いとして…真ん中の式は?」
「まず、横の長さは”![]() ”で、縦の長さは…
”で、縦の長さは…![]() の間では
の間では![]() のところが一番短いでしょう?」
のところが一番短いでしょう?」
「…確かにそうだね」
「だから、縦の長さは![]() に
に![]() を代入した値になるわ。
を代入した値になるわ。
だから、![]() となるわ。あとは、これらを計算するだけ」
となるわ。あとは、これらを計算するだけ」
「あ、そっか!横の長さは区間の長さで、縦の長さは”区間の最大値”だからこういう風になるんだ!」
「こういう風って…どういうことだ?」
「今、この計算は”青い長方形の面積”の和を計算しているよね。
長方形の面積は縦の長さ×横の長さで求められるけど、横の長さは一つ一つの区間の長さだから![]() 、縦は区間の最大値の
、縦は区間の最大値の![]() となるから、それを掛けるとさっきの計算した形になるってこと!」
となるから、それを掛けるとさっきの計算した形になるってこと!」
「なるほど、確かにな…ん、待てよ?
さっきから面積って言っているけど、今の計算結果って”負の値”だろ?
面積で”負の値”になるのはちょっとおかしいんじゃないか?」
「あ…言われてみると確かにそうだ」
ディーの鋭いツッコミに、アキも考え込んでしまいます。
「これってどういうこと?」
その疑問に…
「それは数正が教えてくれるわ」
数正が答えることになりました。
「…まぁ、面積という言い方をするなら、![]() 軸より下なら
軸より下なら![]() 、上なら
、上なら![]() とすればいい。
とすればいい。
そういう”向き付き面積”を考えることもある」
「それで良いんだ!?」
「ん?どういうことだ?」
「あ、えーっとね。
面積って大きさを表すからてっきり正の数しかだめなのかなって思っていたのに、あっさり負の場合も考えれるんだって…」
「まぁ、この考え方は一般的ではないかもしれない。
線形代数学では、2つのベクトルの順番も考慮して面積を決めていくこともあるからな…」
「…その話を聞くのは」
「長くなるから、次に行きましょう」
多少、不安になっていたアキを見て、真理は切り上げることにしました。
「…よかったぁ…これ以上新しい話をすると頭が疲れちゃいそうだったから…」
小さな声でアキはそう話しました。
「計算の続きね。赤い図形の方は…」
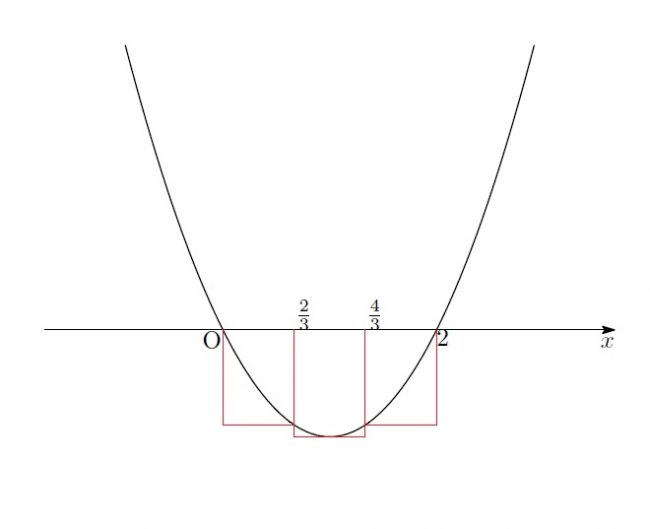
「このようになるわね」
「今度は”区間の最小値”が縦の長さになるんだな。
端の2つはそれぞれ![]() のときに辺の長さが最大になるから、そこの値が高さってことか」
のときに辺の長さが最大になるから、そこの値が高さってことか」
「そういうことよ。大分飲み込めてきたみたいね」
「真ん中のやつは…ど真ん中が一番長いが、これってどんな値なんだ?」
「これは、区間のちょうど中間ね。
今の場合は…」
「”1″だ!」
「その通りよ。
一般にこの形の放物線は”真ん中が最小値”になるわ」
「じゃあ、![]() を代入して…
を代入して…![]() だな…」
だな…」
「情報が揃ったところで、赤い図形の面積を計算してみましょう」
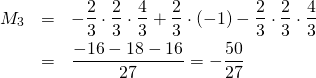
「ここで注目してほしいのは、この2つの面積の間にグラフの面積がある、ということよ。
本来のグラフの面積は
![]()
だけど、これは![]() と
と![]() の間にあるわね」
の間にあるわね」
![]()
「負の値だから、不等式は逆になっているわ」
「図で見ると当然のことだけど、実際に計算するとちゃんと成り立つんだね…」
「![]() 以降のときも確かめましょう」
以降のときも確かめましょう」
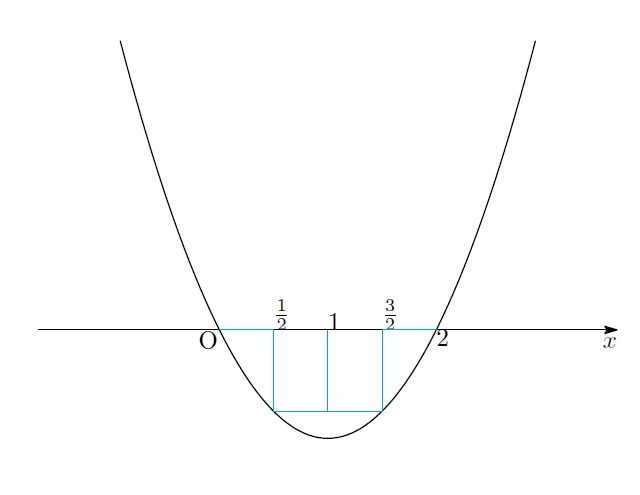
「さっきと違って、今度は真ん中に2つあるんだ」
「まぁ、偶数だからな…」
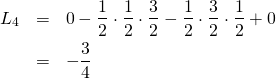
「今度は赤い方ね」
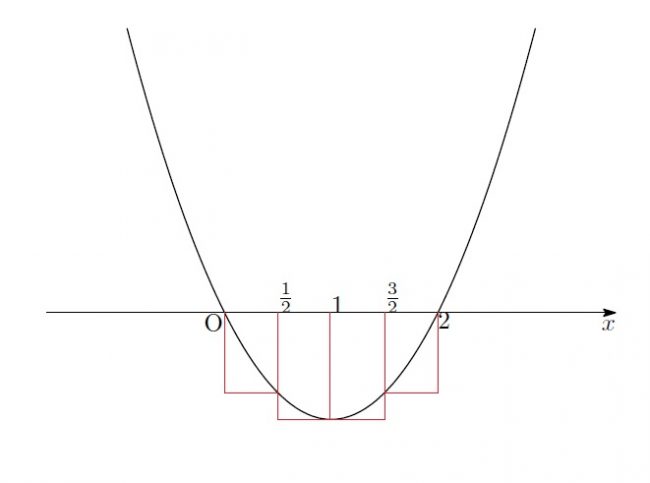
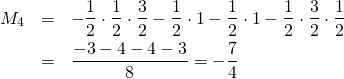
「ここでも、![]() は2つの値の中心になっているね」
は2つの値の中心になっているね」
![]()
「ええ。そしてもう一つ大事なのは、![]() と
と![]() の大小関係。
の大小関係。
![]() より
より![]() の方が、より
の方が、より![]() に近くなっているわね」
に近くなっているわね」
「えー…っと、![]() で
で![]() だから、
だから、![]() の方が小さくて…確かに近くなってる」
の方が小さくて…確かに近くなってる」
「![]() と
と![]() は…
は…
![]() で
で![]() だから、
だから、![]() の方が大きいんだな」
の方が大きいんだな」
「このように、![]() の値が大きくなるほど、段々と
の値が大きくなるほど、段々と![]() と
と![]() の値は近づいていくのよ」
の値は近づいていくのよ」
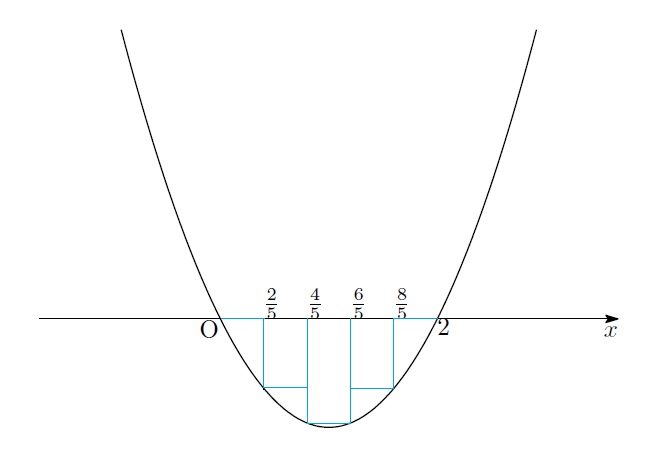
「![]() のとき、青い図形はこうなるわね」
のとき、青い図形はこうなるわね」
「![]() は…」
は…」
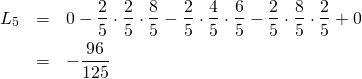
「こうか?」
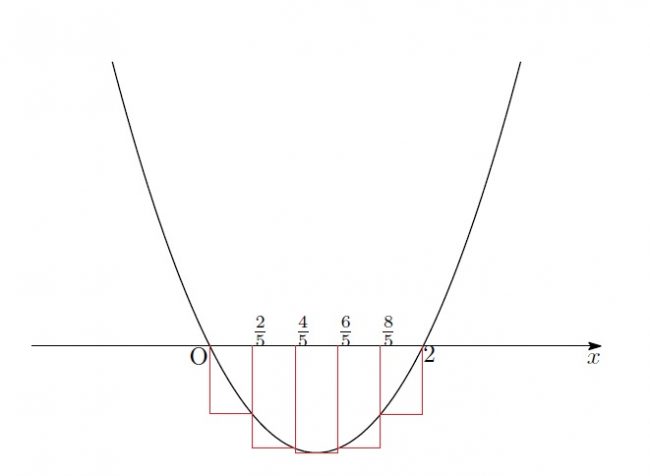
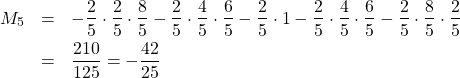
「…![]() はこうか」
はこうか」
「大分計算慣れしてきたわね。![]() のときもやってみましょう」
のときもやってみましょう」
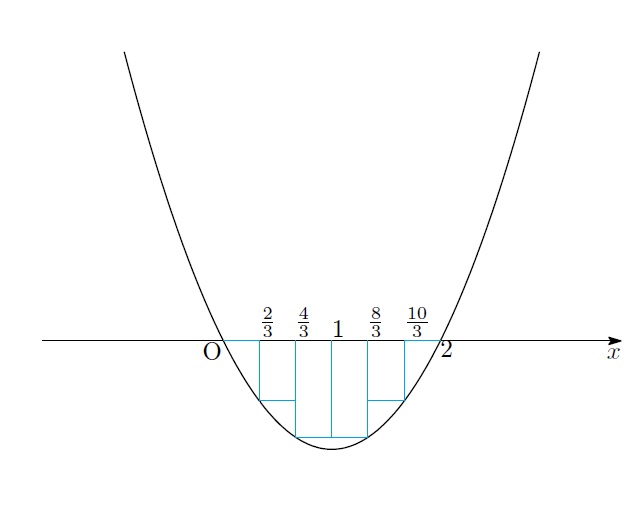
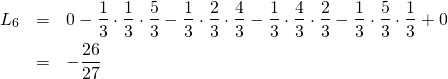
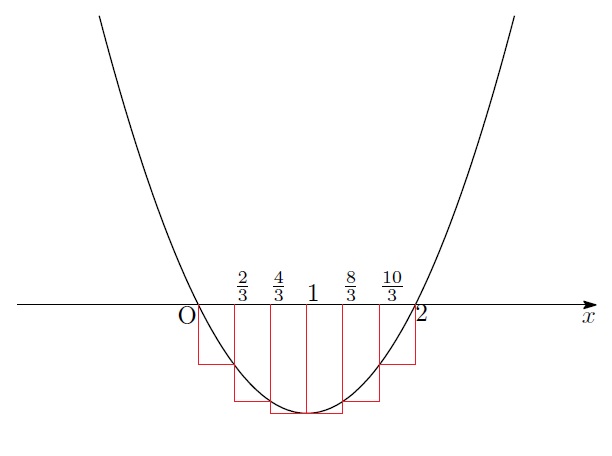
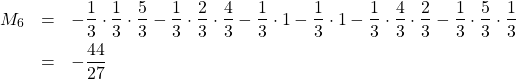
「…ふぅ、計算するのも大変だね」
「確かにそうね。
でも、色々なことに気づけたのではないかしら?」
真理の問いかけを聞いて、二人はそれまでの計算過程をじっと眺めました。
「…これ、![]() を増やしていくほど計算が大変じゃねーか?」
を増やしていくほど計算が大変じゃねーか?」
「なんとも、ディーらしいというか…」
「どういう意味だよ!?」
ディーの感想に、思わずアキが苦笑いしながら答えてしまいました。
「…同感ね」
「「?」」
「それはどっちに対してだ?」
「2人共よ。
アキの言うように、計算が苦手なディーらしい意見だと思うけど、ディーの言うことももっともなのよ。
だからこそ、計算をする際にパターンが必要だし、公式というものがあるのよ」
「…あー、確かに。これをいちいち計算するって考えたら本当に嫌になるわ…。
積分の公式があって良かったぜ、ホント」
真理の意見に、ディーも心底同意していました。
「…それにしても、計算してみると同じものが色々出てるよね」
「どういうことだ?」
今度はアキの気付きに対して、ディーが疑問に思いました。
「うーーん、色々ありすぎて…」
「一つずつでいいわよ」
「うん、まずね…」

「![]() が偶数のときには、最初半分と後の半分はおんなじ図形になっているなって思ったの。
が偶数のときには、最初半分と後の半分はおんなじ図形になっているなって思ったの。
![]() や
や![]() の時には確かにそうなっているけど、それ以上でも成り立つのかな?」
の時には確かにそうなっているけど、それ以上でも成り立つのかな?」
アキの話を聞いて、数正が答えました。
「それは確かに成り立つ。なぜかと言うと、”放物線は軸を対象に線対称”だからだ」
「今の場合は![]() が軸になっているけど、そこで折り返すとちょうど重なるわよね。
が軸になっているけど、そこで折り返すとちょうど重なるわよね。
![]() が偶数のときには
が偶数のときには![]() を境に同じだけ区切れる、言い換えると同じだけ長方形ができるのよ。そして、それはちょうど
を境に同じだけ区切れる、言い換えると同じだけ長方形ができるのよ。そして、それはちょうど![]() で対称になっているわ」
で対称になっているわ」
真理の話を聞いて、少し考えてみるアキ。
「もう少し厳密に説明しよう…![]() とする。
とする。
このとき、![]() と
と![]() 、
、![]() と
と![]() というように…」
というように…」
![]()
「という対応がある。先程の区間で言うと![]() となる」
となる」
「…もしかして、![]() と
と![]() 、
、![]() と
と![]() が対応しているってこと?」
が対応しているってこと?」
「そう!そこがポイントだ。![]() と
と![]() が
が![]() を挟んで対応している」
を挟んで対応している」
「じゃあ、もしかして…」
と言って、アキは計算をしてみました。
![]()
「おぉ!![]() と
と![]() のときが同じ値になる!」
のときが同じ値になる!」
「…これって、![]() と
と![]() って対応しているやつを掛けているんだよな。
って対応しているやつを掛けているんだよな。
だったらある意味当たり前じゃないか?同じ値になるの」
と、ディーがツッコみます。
「なかなかいい気付きだな。それが対称性というわけだ」
「あとは…長方形の高さは各区間の端点の値になる。![]() なら小さい方、
なら小さい方、![]() なら大きい方ね。
なら大きい方ね。
そして、それは![]() を対称にして、対応しているところが同じ値になるから…」
を対称にして、対応しているところが同じ値になるから…」
「じゃあ、半分だけ計算すれば求められるんだね!」
「そうだな、まぁ偶数のときだけになるが」
「も~、そういうことは言わなくていいの!数正くん!」
と、アキがちょっと怒ったように話しました。
「あとね、![]() と
と![]() でも同じような数が多いなって思ったの。
でも同じような数が多いなって思ったの。
![]() の方は両端が
の方は両端が![]() になるからなのかもしれないけど、ちょうど
になるからなのかもしれないけど、ちょうど![]() とは長方形
とは長方形![]() つ分の差になっているよね」
つ分の差になっているよね」
「言われてみると…」
とディーが図を見ながらアキの話に同意しました。
「この長方形たちは段々と細くなっていくから、![]() と
と![]() の差は縮まりそうだなって思った!」
の差は縮まりそうだなって思った!」
「お、そういうんだったら、俺ももう一つ気づいたぜ。
![]() を大きくするごとに、確かに
を大きくするごとに、確かに![]() や
や![]() の長方形とグラフの隙間がなくなっていくよな。
の長方形とグラフの隙間がなくなっていくよな。
…まぁ、これは当たり前なのかもしれないが」
ディーも図を見て気づいたことを話しましたが、多少”大したことない”ように言っていました。
「何を言っているのかしら。
確かに区分求積法の説明の時に2つの長方形がグラフに近づく話はしたわ。
だけど、それが実際に成り立つかどうかはわからないのよ」
「連続な関数…厳密には違うが、グラフが繋がっている関数ならこれは成り立つ。
だが、それ以外のものでも成り立つものがあるし、意外とその判定は難しい」
「さっきディーも言ったわよね。青い長方形と赤い長方形の極限が本当にグラフに近づくのかって。
今の関数で実際に近づくことが確かめられた、というのは大きな気付きだと私は思うわ」
「そこまで言われるとなんだか照れるな…」
数正と真理の言葉を聞きながら、少々気恥ずかしさを感じるディーなのでした。
「アキの話も大事だ。今の気付きによって、![]() と
と![]() の差が
の差が![]() を大きくすると
を大きくすると![]() に近づくことも証明できる」
に近づくことも証明できる」
「そうなの?」
「ポイントは、長方形![]() つ分の差であることと、高さの最大値が
つ分の差であることと、高さの最大値が![]() であることだ。
であることだ。
今、長方形の面積が最大になるのは高さが![]() 、幅が
、幅が![]() のとき。そして、
のとき。そして、![]() は長方形2つ分の差であるならば、これは面積が最大になる長方形2つ分より小さいはずだ。よって」
は長方形2つ分の差であるならば、これは面積が最大になる長方形2つ分より小さいはずだ。よって」
![]()
「このような等式が成り立つ。以上より![]() と
と![]() の差は
の差は![]() に収束する。つまり、
に収束する。つまり、![]() と
と![]() は同じ値に収束する」
は同じ値に収束する」
「あっ!それがグラフと![]() 軸で囲まれた面積なんだね!」
軸で囲まれた面積なんだね!」
「ええ、これで区分求積法が成り立つことが示せた、というわけね」
→積分編⑩
この記事を書いたブロガー
-
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。
最近の投稿
 日々感じること2024年11月13日運動不足?
日々感じること2024年11月13日運動不足? 日常生活2024年11月12日最近の直さなければならないところ
日常生活2024年11月12日最近の直さなければならないところ 日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。
日常生活2024年11月11日「考えを間違えてはいけない」という強烈なメッセージ。 日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件
日常生活2024年11月10日神様をいつも考えていたら、色々な祝福が来た件



