真理の森の数学セミナー～積分編Last～ | 摂理研究所/キリスト教福音宣教会

→積分編⑨

「…積分の定義について、まとめましょう。
まず、区間を分割して、区間内の最大値と最小値を高さとする長方形を考える。
その長方形を足していくと、最小値をとった長方形の面積の和はグラフの面積より小さく、最大値の方はグラフの面積より大きい。
そして、この二つの面積が区間を細かく分割するほど一つの値に近づくとき、これを積分ということにする。
もっと大雑把にいうと、大事なのは”グラフを長方形に分割して、それを限りなく細かくしていくこと”よ」

「それが、積分の定義ってわけだな」

ディーが真理の説明を聞いてひとまず納得していました。

「”細かい長方形を足し合わせる”というのが積分の本質よ」

「うん、だいぶ分かってきた！」

アキも元気そうに返事をしました。
そのとき、真理はどことなく”何かを企んでいる”笑みを浮かべつつ続けました。

「…言い換えると、”細かく分割するとグラフに囲まれた図形に近づくよう長方形で囲め”ば良いのよね」

「…た、確かにそうだね」

その様子を見ながら、若干まごつくアキ。

「…真理、いったい何を考えているんだ？」

数正もこの後の展開が分からず、戸惑っていました。
最も、このセミナーでは”真理の予想外の話”はよくあることなのですが。

「…おそらく、普通だったら”区間求積法”の定義通りに長方形の面積の和を計算して、その極限を確かめるのが筋でしょうね。
だけど、それだと複雑すぎて私の伝えたいことが分かりにくいわ。
それに…」

そこで一旦区切り、真理は皆を見ながらこう言いました。

「流石に時間が掛かりすぎね。そろそろ話をまとめた方が、お互いのためでしょう？」

「…まぁ、な」

その言葉に思わず同調したディー。
実際、真理が自分の発見について説明をしてから数十分が経過していました。
アキもディーも、新しい概念を理解するためにかなり頭を使って疲れてます。

「大丈夫。この後の話は簡単だから」

それを分かってか、真理は微笑みながらそう話しました。

「さて、これから”1/6公式”の”積分の定義”を使った証明を始めましょう。
さっきも話したように、”積分の定義”とは”グラフで囲まれた図形を細かく分割する”ことであり、細かく分割した図形を長方形で近似すること。
“区間求積法”では分割した区間での最小値、最大値を高さとした長方形で近似したのだけど…」

そういって、真理は一つの図形を黒板に書きました。

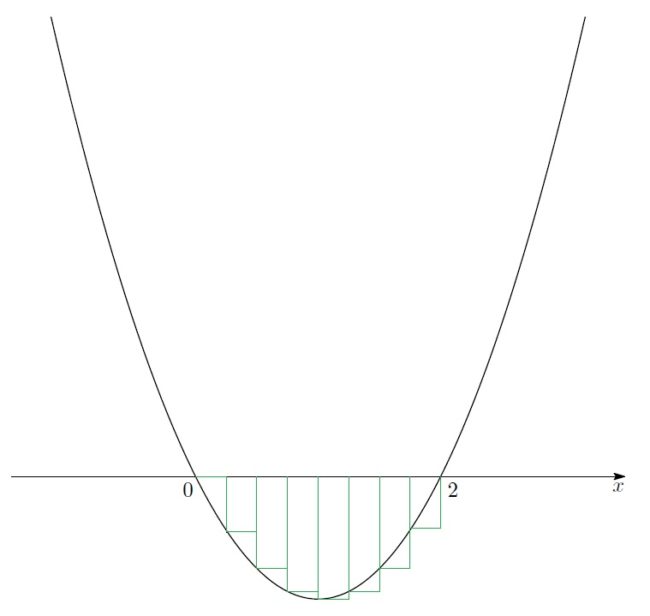
「今から計算するのは、次のような近似の仕方よ」

「これは…」

「区間の端っこを高さにしている？」

3人は真理が書いた図を見ながらびっくりしていました。

「その通りよ。今から考えるのは”各区間の端点の値を高さとした長方形”の和の極限」

「…え、これって大丈夫なの？」

「それについて、細かくは後で話すとして…。
結論から話すとこの図形は最終的にはグラフの面積と一致するわ」

「…どうしてなのか、聞いてもいい？」

「そうね…。この図形を見ると左半分が” $L_n$ ”、右半分が” $M_n$ ”に分かれているのが分かるかしら？」

「あ、確かにそうなってるね」

「放物線は軸より左では単調減少、軸より右では単調増加となるから、軸より左は区間の左端が最小、右は区間の左端が最大になるわけ」

「そうなると、さっき計算したみたいに…」

と、ディーはさっき計算したときのことを思い出していました。

「そう、直感的には”細かく分割するほどグラフに近づいていく”となるわけ。
まぁ、これはあくまで直感に過ぎないのだけど…」

「う～ん…なんとなくは分かったような…」

「ひとまず、計算してみましょう。
区間の長さは $\beta-\alpha$ で、これを $n$ 等分するから…」

「長方形一つの横の長さは $\frac{\beta-\alpha}{n}$ ？」

「ええ、それで合ってるわ。
そして、分割した $k$ 番目の区間は $\alpha+\frac{\beta-\alpha}{n}(k-1)\le x\le \alpha+\frac{\beta-\alpha}{n}k$ となるわね」

「うーん…これは…」

アキは数式を見ながらしばし悩んでいました。

「 $k$ を具体的な値で考えてみると良いわ」

「 $k=1$ 、つまり”1番目の区間”は…最初が $\alpha$ で、終わりは区間の幅が $\frac{\beta-\alpha}{n}$ だから、 $\alpha+\frac{\beta-\alpha}{n}$ か。
さっきの式に $k=1$ を代入してみると…お、確かに一致してるぜ」

「あとは、 $\frac{\beta-\alpha}{n}$ を加えていけば良いから… $n$ 番目のときは $\alpha+(\beta-\alpha)=\beta$ になって、確かによさそうだ！」

具体的に計算していって、2人は納得できたようです。

「今は各区間の始点、左端の値を高さとして考えているから高さは…」

$\begin{eqnarray*} &&\left(\alpha+\frac{\beta-\alpha}{n}(k-1)-\alpha\right)\left(\alpha+\frac{\beta-\alpha}{n}(k-1)-\beta\right)\\ &=&\frac{\beta-\alpha}{n}(k-1)\left(\frac{\beta-\alpha}{n}(k-1)+\alpha-\beta\right)\\ &=&\frac{\beta-\alpha}{n}(k-1)\left(\frac{\beta-\alpha}{n}(k-1)-(\beta-\alpha)\right)\\ &=&\frac{\beta-\alpha}{n}(k-1)(\beta-\alpha)\left(\frac{k-1}{n}-1\right)\\ &=&\frac{\beta-\alpha}{n}(k-1)(\beta-\alpha)\frac{k-1-n}{n}\\ &=&\frac{(\beta-\alpha)^2}{n^2}(k-1)(k-1-n) \end{eqnarray*}$

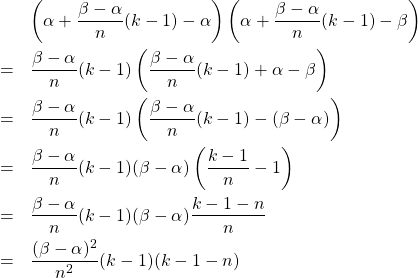
「となるわね。ちょっと難しかったかしら…」

「…いや、なんとかついていけてるぜ」

少し自信なさそうですが、ディーはそう話しました。

「以上から、一つの長方形の面積は」

$\frac{\beta-\alpha}{n}\times\frac{(\beta-\alpha)^2}{n^2}(k-1)(k-1-n)=\frac{(\beta-\alpha)^3}{n^3}(k-1)(k-1-n)$

「となるわ」

「…そっか、 $\beta-\alpha$ は区間の長さで、それが三乗されるのは長方形の面積から来ているんだね」

$\frac{1}{6}$ 公式と見比べながらアキがつぶやきました。

「今の場合長方形の高さが2次関数の値だから、横の区間の長さと合わせて三乗になるのよ」

「ふーん…こう考えると、数式一つ一つに意味があるんだね」

「そこを分かるのが数学の楽しみだって、私は思うわ」

そう、真理は答えて…続きの式を書きました。

「これで、 $\frac{1}{6}$ 以外の部分の意味は見えてきたわね。残る $\frac{1}{6}$ は…」

$\sum_{k=1}^{n}\frac{(\beta-\alpha)^3}{n^3}(k-1)(k-1-n)$

「今出た長方形の面積を全て足していくことで現れるわ」

「いよいよ、最後の計算ってわけだな」

真理の話を聞きながら、ディーは少し楽しみそうに話しました。

「まず、 $(k-1)$ が出ているのは少し見にくいから、 $\sum$ の下の変数を少し変えるわね。
具体的には $l=k-1$ と置くわ」

「そうすると…」

と言いながら、アキが一つ一つ置き換えました。

「 $k=1$ のときは $l=1-1=0$ で、 $k=n$ のときには $l=n-1$ だから」

$\sum_{k=1}^{n}\frac{(\beta-\alpha)^3}{n^3}(k-1)(k-1-n)=\sum_{l=0}^{n-1}\frac{(\beta-\alpha)^3}{n^3}l(l-n)$

「こうだね！」

「ええ、その通り。これで少し見やすくなったわね。
それから、 $\frac{(\beta-\alpha)^3}{n^3}$ の部分は…」

「確か、 $l$ が変わっても、変わらずに出てくるんだったか？」

$\sum_{l=0}^{n-1}\frac{(\beta-\alpha)^3}{n^3}l(l-n)=\frac{(\beta-\alpha)^3}{n^3}0\times(-n)+\frac{(\beta-\alpha)^3}{n^3}1(n-1)+\cdots$

「そう。だから、この部分を括るようにして、 $\sum$ の前に出せるわ」

$\sum_{l=0}^{n-1}\frac{(\beta-\alpha)^3}{n^3}l(l-n)=\frac{(\beta-\alpha)^3}{n^3}\sum_{l=0}^{n-1}l(l-n)$

「だから…」

$\sum_{l=0}^{n-1}l(l-n)$

「この部分を計算すればいいの。あとは…」

$\begin{eqnarray*} \sum_{l=0}^{n-1}l(n-l)&=&\sum_{l=0}^{n-1}(l^2-ln)\\ &=&\sum_{l=0}^{n-1}l^2-n\sum_{l=0}^{n-1}l\\ &=&\frac{n(n-1)(2n-1)}{6}-n\times\frac{n(n-1)}{2}\\ &=&\frac{n(n-1)}{6}((2n-1)-3n)\\ &=&-\frac{1}{6}(n-1)n(n+1) \end{eqnarray*}$

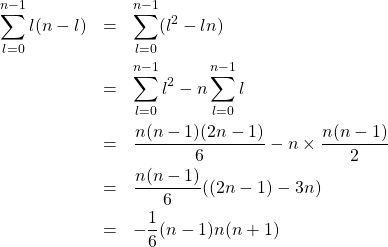
「と、このように計算できるわ」

「なぁ、途中のこの辺りなんだが…」

とディーが計算について真理に尋ねている間、数正は…

「そうか…この部分で $\frac{1}{6}$ が出ているんだな。さらに、残りの部分は…」

一人、計算の続きをしながら感嘆していました。

「…だから、通分するときに分子にも $3$ を掛けている。
$n(n-1)$ の部分は共通しているから括れて、残りが $3n$ というわけ」

「おお、少し分かった気がするぜ」

「じゃあ、締めくくりましょう。
今の計算で…」

$\frac{(\beta-\alpha)^3}{n^3}\sum_{l=0}^{n-1}l(l-n)=-\frac{(\beta-\alpha)^3}{n^3}\frac{1}{6}n(n-1)(n+1)$

「となるわね。最後に分割を細かくするから、区間の数 $n$ を大きくするのよ。
つまり、 $n\rightarrow\infty$ … $n$ を限りなく大きくしたときの極限を計算する」

$\lim_{n\rightarrow\infty}-\frac{(\beta-\alpha)^3}{6n^3}n(n-1)(n+1)$

「ちょうど分母に $n$ が3つ出ているから、 $n$ と $n-1$ と $n+1$ 、一つ一つを $n$ で割ってあげましょう」

「 $n$ を $n$ で割ると $1$ になるね！」

$\lim_{n\rightarrow\infty}-\frac{(\beta-\alpha)^3}{6n^3}n(n-1)(n+1)=\lim_{n\rightarrow\infty}-\frac{(\beta-\alpha)^3}{6}\left(1-\frac{1}{n}\right)\left(1+\frac{1}{n}\right)$