【数学小説】真理の森の数学セミナー～積分編⑤～

SHARE

→積分編④

「それでは、これから”\frac{1}{6}公式”について私が気づいたことを説明するわ」

真理が黒板の前で自分が分かった、「森の中で見た」ものについて語りだそうとしていました。

「…それなんだけどよ。俺たちも見つけたんだ！
“\frac{1}{6}公式”の由来」

「へぇ…まず、そっちを先に聞かせてくれる？」

「ああ！数正が”\frac{1}{6}公式”の部分積分法を使った証明を説明して…」

真理が聞く状態になったのを見て、ディーがこれまで三人でしてきたことについてかいつまんで説明しました。

「…部分積分法を使ったんだ」

「ああ、アキがとても面白い発見をしてくれてな…」

「面白いって…ちょっと、照れるよー」

「それでな、(x-\alpha)を2回積分するから

    \[\frac{1}{2}\times\frac{1}{3}=\frac{1}{6}\]

ってなることに俺が気づいたのさ。これが”\frac{1}{6}公式”の\frac{1}{6}の意味じゃないかって」

「なるほど。2回積分するから、\frac{1}{6}なのね。
確かにそれも面白いわ」

真理はその発見を喜んで聞いていました。そして、自分の発見を語り始めます。

「”\frac{1}{6}”という数字を見て、似たような数式がなかったか、色々考えていたのだけど…」

それから、真理は黒板にある数式を書き始めました。

    \[\sum_{k=1}^n k^2=\frac{n(n+1)(2n+1)}{6}\]

「私はこの公式が思い浮かんだの」

「…2乗和の公式か！」

「”2乗和”？」

数式を見て唸る数正と、彼の言葉に引っ掛かるアキ。

「この式の左辺はね、
“1番目からn番目までの平方数の和”
を表しているの。たとえば…n=3のときは」

    \[\sum_{k=1}^3 k^2=1^2+2^2+3^2\]

「となるのよ。実際に計算すると…」

「…1+4+9で14だね」

と、アキがノートに計算して答えました。

「一方、右辺の式にn=3を代入してみると…」

    \[\frac{3\times4\times7}{6}=14\]

「さっきと同じ結果になってる！」

「これはnにどのような値を代入しても等式が成り立つわ。
言い換えると、”1番目からn番目までの平方数の和”を計算する代わりに、右辺の式を計算すればいいというわけ。
これを”2乗和の公式”という」

「…2乗を足すから2乗和なんだね」

「その通りよ」

「そういえば…”\frac{1}{6}公式”は2次関数、2乗が出てくるな」

「ええ、この似ているところから2乗和の公式と”\frac{1}{6}公式”が何か関係があると感じたのよ」

「でもさ…」

と、ディーが訝しげに口を挟みました。

「確かに2乗は出るけど、同じ形とは言えないだろ？
それはどうなるんだ…？」

「そう、これはあくまで直感。
それを確認するために…私は”積分の定義”に立ち返って計算したのよ」

「積分の”定義”？」

アキが”定義”という言葉を聞いてキョトンとしていました。

「”関数の定積分はグラフに囲まれた面積になる”という話は皆も聞いていると思うけど、それにはちゃんと理由があるのよ。それが”積分の定義”」

「それって一体…？」

「順を追って説明していくわ」

と話しながら、真理は黒板に関数のグラフを書き出しました。

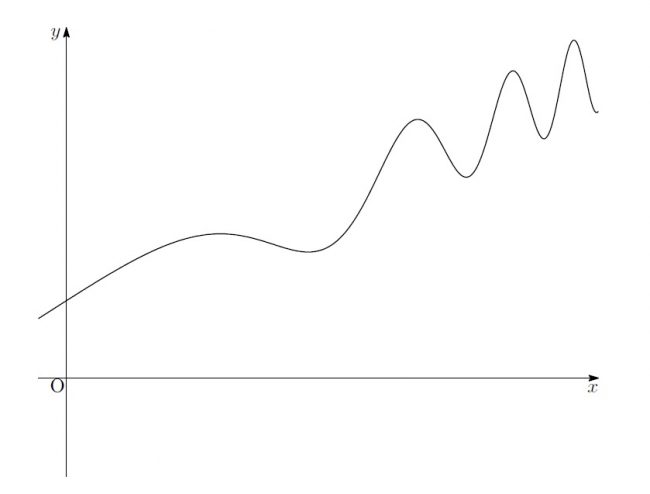
そして、聞いている三人に問いかけました。

「今このグラフが表す関数の式は全く分からないとしましょう。
その時、」

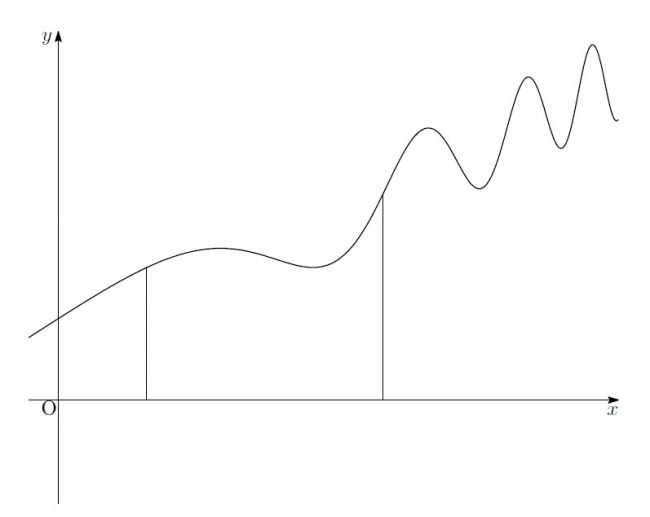
「こういう風にグラフと直線で囲まれた面積を求めるとしたら…貴方達はどうする？」

「はぁ？そんなの積分するに決まってるだろ…」

「どうやって？」

「どうやって、って…」

とディーはしばし考えて…気づきました。

「…どうやるんだ？式分からないのに」

そもそも数式がないから積分した結果が分からないことに。

「この関数の値は分かるの？」

「それは分かるとしましょう。この関数は今のグラフを使って、xに適当な数を代入するとちゃんと値は決められる」

「うーん…」

アキとディーの二人が悩んでいる一方、数正は

「なるほどな…」

とつぶやきました。
数正はこの答えを知っていました。これから真理が話そうとしていることも…。
数正が感嘆していたのは「”そこに至るアプローチ”の巧みさ」でした。

「もっと具体的にしましょうか。
たとえば、このグラフが表す関数は

    \[\sin(e^x)-x+1\]

としましょう。これは積分できるかしら？」

「………はぁ！？」

「…すごい複雑…」

「…」

三人は真理が書いた式を見て思い思いの反応をしていました。
驚くディー、困惑するアキ、そして…

「…”e^x”が”\sin”の中にある…ということは置換積分か…t=e^xとするとdt=e^xdxより…そうするとこの関数の積分は\frac{\sin t}{t}の積分と同値…これは…」

数正は一人頭の中で式変形をしていました。
アキは彼の表情を伺うように尋ねました。

「…できそう？」

「後ろの式は多項式だから簡単に積分できる。問題は、最初の式だ。
結論から言うと…この積分は俺の知る限りでは初等関数で表せない」

「初等関数？」

「高校で習った”多項式、三角関数、指数関数、対数関数”、それから”\sqrt{x}等の無理関数”や”分数関数”のことだ。基本的に俺達が微分積分学で考えるのはこれくらいだ」

「…まぁ、大学では”逆三角関数”とか”\sinh”なんてのもあるけれどね」

数正の答えに真理が付け加えました。

「これらの関数では最初の関数の積分を表すことはできない。
だから…”積分した値を明示的に書くことはできない”、もっと端的に言えば”俺達が習った範囲では積分できない”ということになる」

「マジかよ…」

数正の結論に頭を抱えてしまったディー、それを見ながら真理が説明を続けました。

「私達が高校で習った積分は”結果が数式で表せるもの”だったのよ。
でも、そのような関数は実はかなり珍しい。このようにちょっと複雑にするだけで積分の結果は分からなくなってしまう」

ここまで話して、真理はひと呼吸置きました。
今までの話を三人が飲み込めたタイミングを見て

「それでは改めて…
この関数のグラフで囲まれた面積は、どうやったら求められるかしら？」

再び、問いかけました。

→積分編⑥

→まとめへ戻る

この記事を書いたブロガー

sato
「素直に、深く、面白く」がモットーの摂理男子。霊肉ともに生粋の道産子。30代になりました。目指せ数学者。数学というフィールドを中心に教育界隈で色々しています。
軽度の発達障害(ADHD・PD)&HSP傾向あり。

前の記事

聖書に出てくる「揺祭」って何？

次の記事

【数学小説】真理の森の数学セミナー～積分編⑥～